ASTRA Benefits
Basic measurements
Advanced analyses
Polymer characterization
Dynamic light scattering
21 CFR Part 11 compliance
Request Info
Molar Mass and Size via Light Scattering
Wyatt Technology revolutionized chromatographic analysis of macromolecules by making accurate measurement of molar mass via light scattering a practical reality. ASTRA brings that revolution to you tempered with decades of experience. Consider some of the features that tap into light scattering's full potential while making it easy to use:
Visual analysis
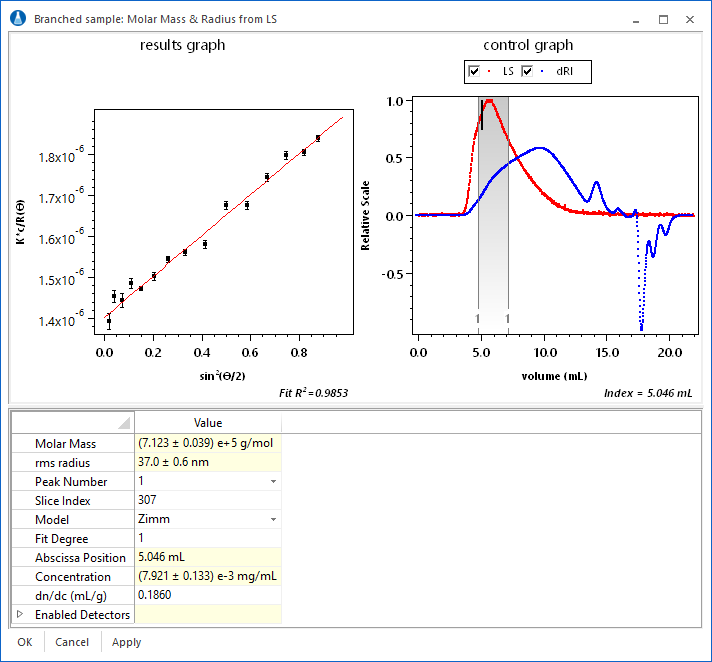
The light scattering analysis view in ASTRA provides the tools to analyze your data easily. Molar mass and radius are instantly calculated and displayed for each slice. Slices can be selected directly from the chromatogram. The fit to the angular variation can be assessed on a slice-by-slice basis. In addition, individual detectors can be enabled or disabled, with instant feedback.
ASTRA supports several sophisticated models for analyzing the angular variation in the light scattering intensity to retrieve size information. Please see the section on particle analysis for details.
Light Scattering Instrument Support
Most other software packages that process light scattering data do not offer native support of light scattering instrumentation. Instead, they require that polymer standards be used to calibrate the instrument. This removes the fundamental advantage of light scattering to measure the molar mass directly, and instead ties light scattering to all of the weaknesses of column calibration.
ASTRA offers native support for light scattering instrumentation. Polymer standards are not needed to calibrate an instrument. Instead, a simple measurement of the fundamental scattering from a pure solvent is used to convert all further measurements into the native scattering units of Rayleigh ratio. No assumptions are necessary - in combination with a concentration detector, ASTRA measures molar mass directly.
Advantages of light scattering
Light scattering stands alone in its ability to measure the molar mass of macromolecules in solution both accurately and quickly:
- As opposed to mass spectrometry, light scattering can determine molar mass and aggregation state.
- As opposed to analytical ultracentrifugation, light scattering can measure molar mass and aggregation state in real time for fractionated samples.
- As opposed to column calibration, light scattering requires no outside standards, nor does it make any assumptions about how the sample elutes.
In addition to molar mass, light scattering also measures size. For more information on how light scattering works, please visit our Theory section.
Distributions
Most chromatography analysis programs calculate the properties of a sample for a single peak (i.e., a range of elution volumes). For example, one might determine the average molar mass, intrinsic viscosity, or hydrodynamic radius for a peak. This is a very powerful way to characterize different fractions of an eluting sample.
Another powerful way to interpret data from a fractionated sample is to consider distributions of measured quantities. For example, one might want to know the fraction of a sample that has a molar mass within a certain range. The way to do this is to calculate a cumulative distribution of molar masses.
To calculate a cumulative distribution, the following steps are taken:
- The total mass of the eluting sample is calculated. If the concentration is measured at each eluting slice, then the total mass is equal to the sum of the concentration measurements times the eluting slice volume.
- The molar mass is calculated for each eluting slice using a DAWN or miniDAWN MALS detector.
- The resulting molar masses and the measured concentration at that slice are then sorted by ascending mass.
- The weight fraction of sample with a certain molar mass or lower is then calculated by summing all of the concentrations up to the specified molar mass, multiplying this sum by the volume of the eluting slice, then dividing by the total mass of the sample.
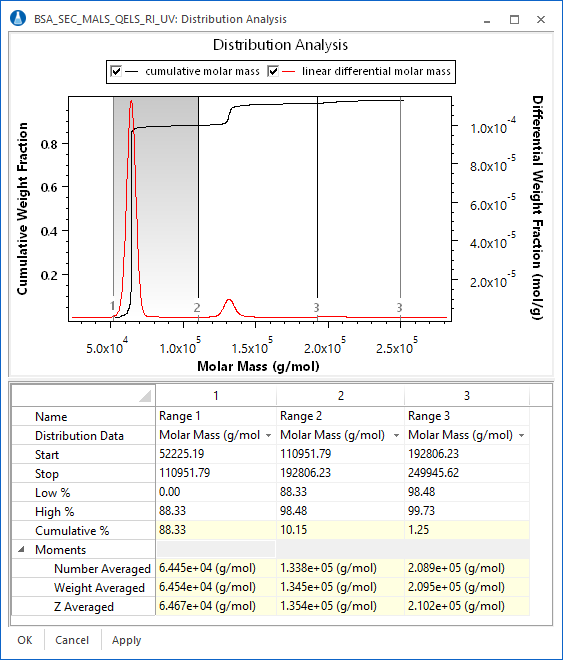
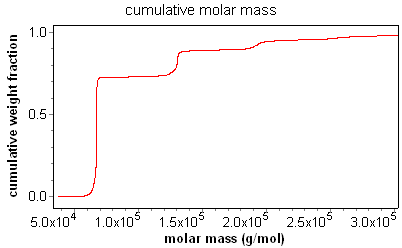
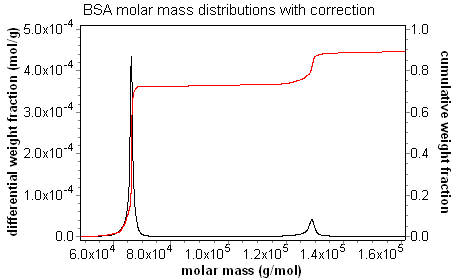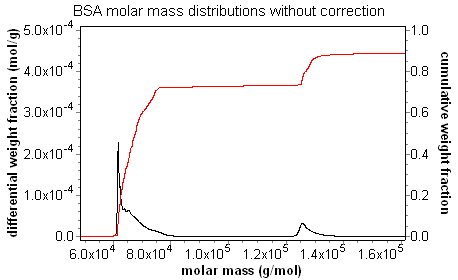
The result of this procedure for a fractionated BSA sample is shown in the figure below. As can be seen, there is a "stair-step" pattern, with the steps occurring at the mass for each oligomer. It is easy to determine the fraction of sample in each oligomer simply by looking at the step height.
The differential distribution is exactly that. One way to calculate a differential distribution is to take the differential of the cumulative distribution. This can be seen clearly in the overlay below of the cumulative and differential distributions of a fractionated BSA sample. The differential distribution provides a revealing visual representation of the weight fraction of a sample within a certain molar mass range, and provides information on the ultimate resolution of the entire fractionation, data collection, and analysis system.
The calculation of differential distributions has traditionally been a tricky affair. The simplest approach is to fit the resulting data to a monotonic function, and then use the analytical expression for the fit function to calculate the differential distribution directly. This technique has severe limitations (a.k.a. it simply does not work), particularly for narrow peaks, oligomer sequences, and nonstandard fractionation techniques. Wyatt Technology has implemented a proprietary adaptive binning algorithm to accurately calculate differential distributions without fitting the data. The results are truly amazing. It is a snap to calculate differential distributions for narrow standards and oligomer sequences.
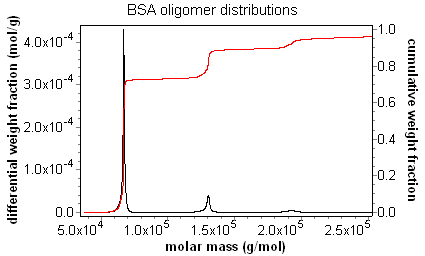
ASTRA capitalizes on this important functionality by presenting users with the powerful distribution analysis procedure. As can be seen in the screen shot, the fraction of a sample in a certain mass range can be ascertained simply by dragging a region in the combined distribution graph. In this case, the weight fraction of BSA monomer, dimer, and trimer can be determined and reported. In addition, when combined with ASTRA's number density calculations, the number fraction of a sample in a certain size range can be determined with the distribution analysis procedure.
Why the band broadening correction is essential for distributions:
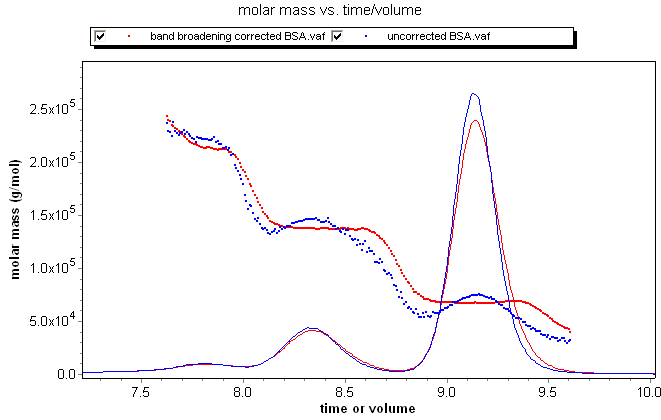
Calculated distributions present an accurate map of the computed value for each eluting slice. As shown in the discussion on band broadening, setting a peak region can compensate for the "grimace" in molar mass across the peak; the average molar mass is correct. There is no way to compensate for the "grimace" in the distribution plot, however. Without the band broadening correction, the values from a sharp, monodisperse peak are artificially spread out. There is an apparent loss in resolution. With the band broadening correction, the true distribution becomes apparent, and resolution is restored. The animation below of BSA oligomers measured with and without the band broadening correction demonstrates clearly that the band broadening correction is necessary to determine accurate distributions.
Zimm Plot/Second Virial Coefficient
Light scattering can be used to measure the second virial coefficient (A2) of a macromolecule. A2 is a measure of macromolecular self-interaction, and is a useful parameters for optimizing crystallization and formulation conditions of proteins.
Global fitting
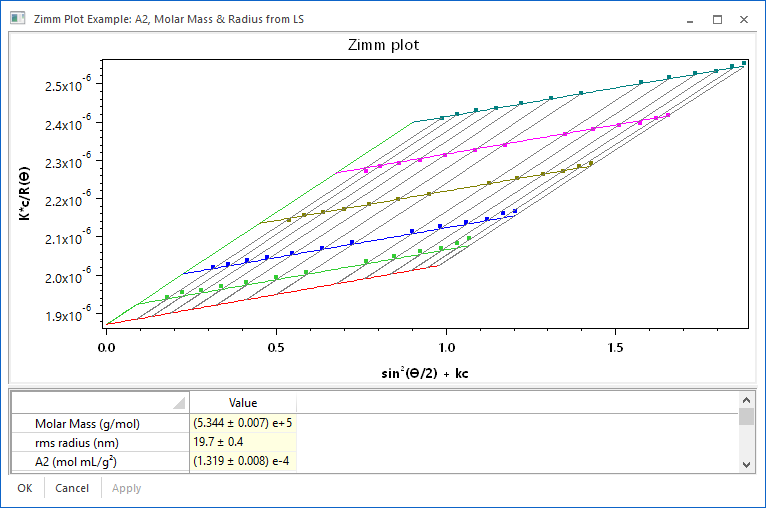
Traditional Zimm plots involved multiple fits to multiple sets of data, and extrapolations to zero scattering angle and concentration. ASTRA employs a proprietary global fitting technology that upgrades the Zimm plot to a more robust, modern analysis. The global fitting technology removes all extrapolations from the Zimm plot method, helps identify inconsistent data sets, and provides more precise and robust results for A2. As with all analysis procedures in ASTRA, the global fit view (shown at right) offers immediate visual confirmation of fit quality using a new visual representation of the Zimm plot. Parameters can be changed in the grid view, and fit results viewed immediately.
Traditionally, A2 was measured using a painstaking process of preparing multiple concentrations of a sample, and then making multiple measurements to construct a classic Zimm plot. Wyatt Technology is committed to bringing this technology into the 21st century, particularly since it is of growing importance to the protein characterization community. Some of the avenues that we have implemented or are exploring include:
Online A2 determination
ASTRA supports the analysis of rapid injections of small volumes of a sample, ideally prepared in an autodilution process in an autosampler. This proprietary online analysis can retrieve A2 using a fraction of the sample needed for traditional measurements, and supports automation and high-throughput studies.
Protein Conjugate and Copolymer Analysis
It is possible to determine the molar mass, size, and relative polymer fractions of a copolymer using light scattering. All that is required are two additional detectors that have differing sensitivities to the constituent polymers. Traditionally, light scattering has been used in conjunction with an RI and UV detector for this purpose.
An important class of copolymers are protein conjugates. For example, researchers often need to determine the fraction of protein in glycosylated and pegylated proteins, as well as membrane protein-detergent complexes. ASTRA has native support for protein conjugate and copolymer analysis using a light scattering detector in conjunction with a UV and RI detector.
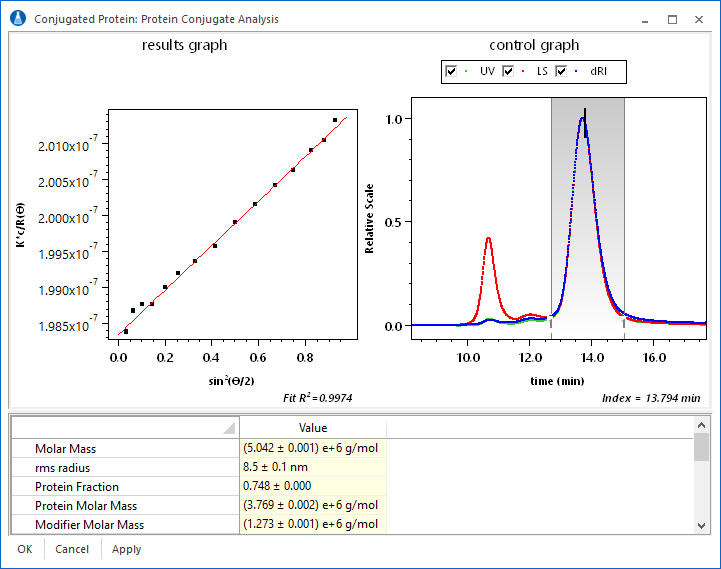
The interface for the protein conjugate analysis is easy to use. Once the dn/dc and UV extinction values for the protein and modifier have been entered, it is possible to view the total molar mass and protein fraction on a slice by slice basis. ASTRA calculates the size of the complex and molar masses of the complex and the constituents. In addition, the concentration and calculated dn/dc values are displayed for that elution volume.
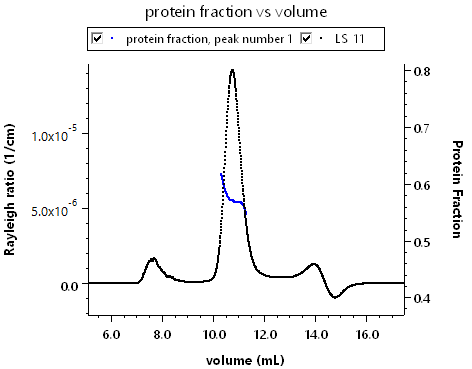
The protein conjugate analysis is a rich example to display the powerful custom graphing capabilities of ASTRA. Consider the plot at right of protein fraction vs. elution volume for a membrane protein-detergent complex. Any data that ASTRA calculates can easily be plotted in this way.
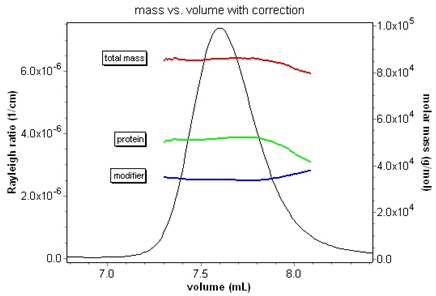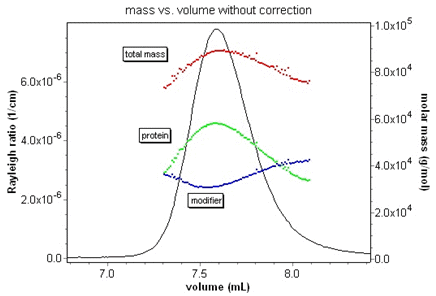
Since the protein conjugate analysis uses three detectors in series, it is absolutely essential to correct for band broadening effects to get accurate results. Consider the animation below of the relative protein and modifier fractions for a membrane protein-detergent complex. The protein fraction and mass should be constant over the eluting peak. Without the band broadening correction, it is impossible to ascertain this. With ASTRA and the correction, the true fractions are instantly revealed.
dn/dc and UV Extinction Determination
ASTRA has several different methods for determining the dn/dc or UV extinction coefficients for your sample:
Direct measurement
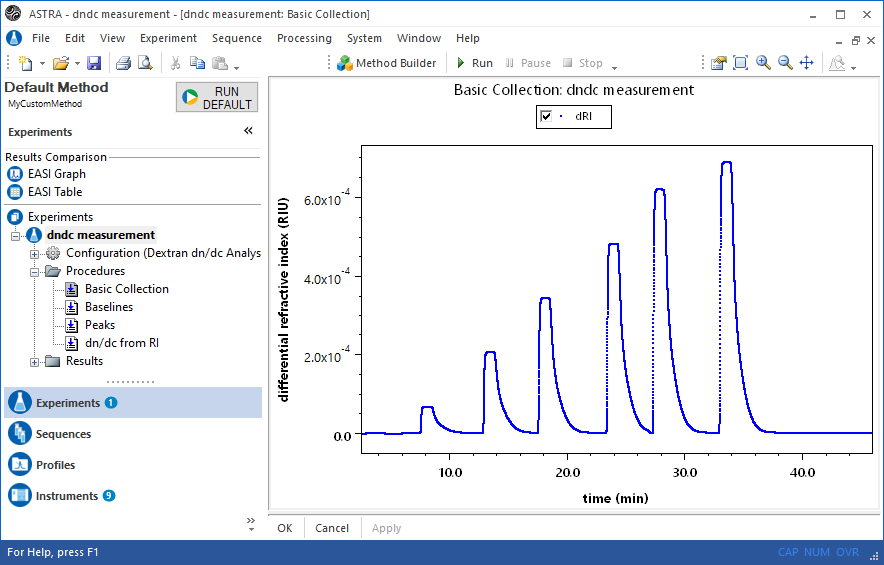
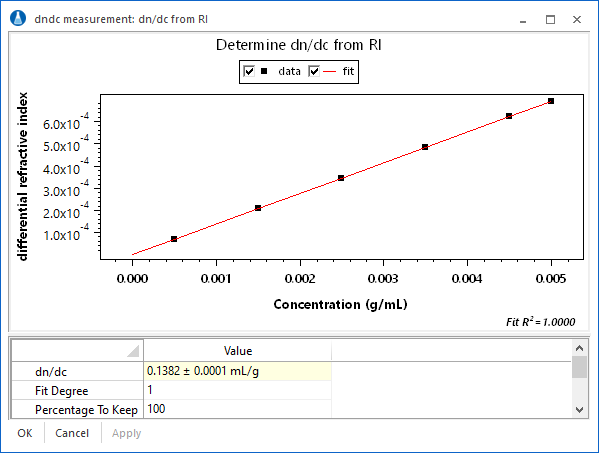
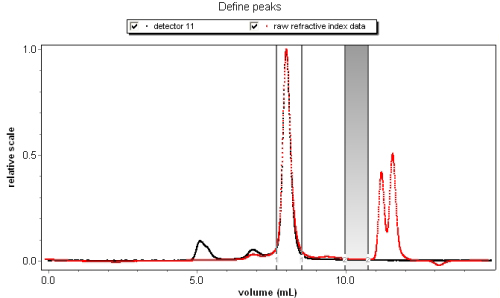
Inject aliquots of known concentration into an Optilab refractometer or UV detector. ASTRA provides experiment methods for determining dn/dc or UV extinction coefficients. Define baselines, set peak regions with concentrations, then view the corresponding analysis procedure to determine dn/dc or UV extinction.
On-line measurement
If the assumption can be made that 100% of the injected mass reaches the Optilab or UV detector, it is possible to calculate the dn/dc or UV extinction coefficient on-line.
Alternately, if an Optilab and UV detector are used in combination, and the dn/dc value is known for the sample, ASTRA can calculate a UV extinction coefficient for the sample.
RI Calibration
If a third-party RI detector is being used, ASTRA provides an experiment template to calculate the RI calibration constant for the analog input signal.
Absorption Correction
Multi-angle light scattering (MALS) analysis is based on the intensity of scattered light as measured by an array of photodiodes. If the correct mass of a sample is to be measured, we must account for known variations in the intensity of the laser source so that we do not incorrectly attribute such changes to the sample being analyzed.
ASTRA® has the ability to account for variations in the laser intensity due to power fluctuations by dividing the measured signal by the laser monitor. ASTRA has now been extended to account for changes in measured intensity due to absorbance by the sample. This is accomplished by applying an additional correction to the measured intensity based on changes in the forward laser monitor signal.
Data Collection Requirements
To apply the Forward Monitor Correction to a sample, the forward monitor signal must be measured at the time of data collection. The DAWN® and the miniDAWN® measure the forward monitor signal with every collection.
Analysis
The standard laser monitor correction works well when there is no interaction of the signal with solvent or sample. This is typically not the case with the forward monitor correction, because the presence of sample directly affects the measured intensities. If the collection is stopped during a solvent peak, or when the baseline is otherwise changing, the measurement of average monitor value is inaccurate. Therefore, the forward monitor correction requires the user to specify a peak range for the pure solvent. The correction uses this 'pure solvent' peak to compute the forward monitor average.
Results
The forward monitor correction adjusts the measured light intensity based on the change in the forward monitor, in proportion to the square root of the ratio between the forward monitor signal and the average forward monitor signal. Consequently, small fluctuations in forward monitor signal are expected to yield small changes in the measured molar mass. The following examples illustrate these effects.
Consider an absorbing sample, shown below, where the forward laser monitor (measured on aux channel 2) has an average value of ~3.05 V, but drops to ~2.35 V in the presence of the absorbing sample (a drop of ~23%). Consequently, the expected change in molar mass should be around that value. A comparison of the sample with and without the forward monitor correction is shown below.
| Absorbing Sample | |||
|---|---|---|---|
| Sample | Sample with Correction | Change | |
| Mn | 2.157e+5 (0.3%) | 2.598e+5 (0.3%) | 20% |
| Mw | 2.166e+5 (0.3%) | 2.615e+5 (0.3%) | 21% |
| Mz | 2.174e+5 (0.6%) | 2.629e+5 (0.7%) | 21% |
| Mw/Mn | 1.004 (0.4%) | 1.007 (0.5%) | - |
| Mz/Mn | 1.008 (0.6%) | 1.012 (0.8%) | - |
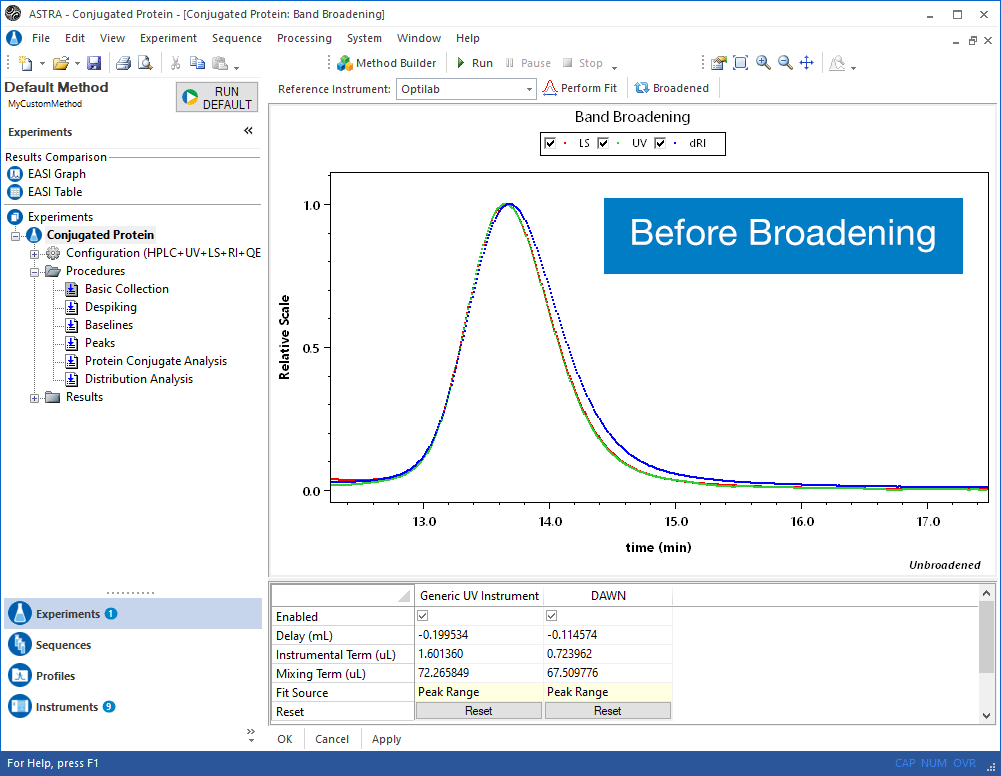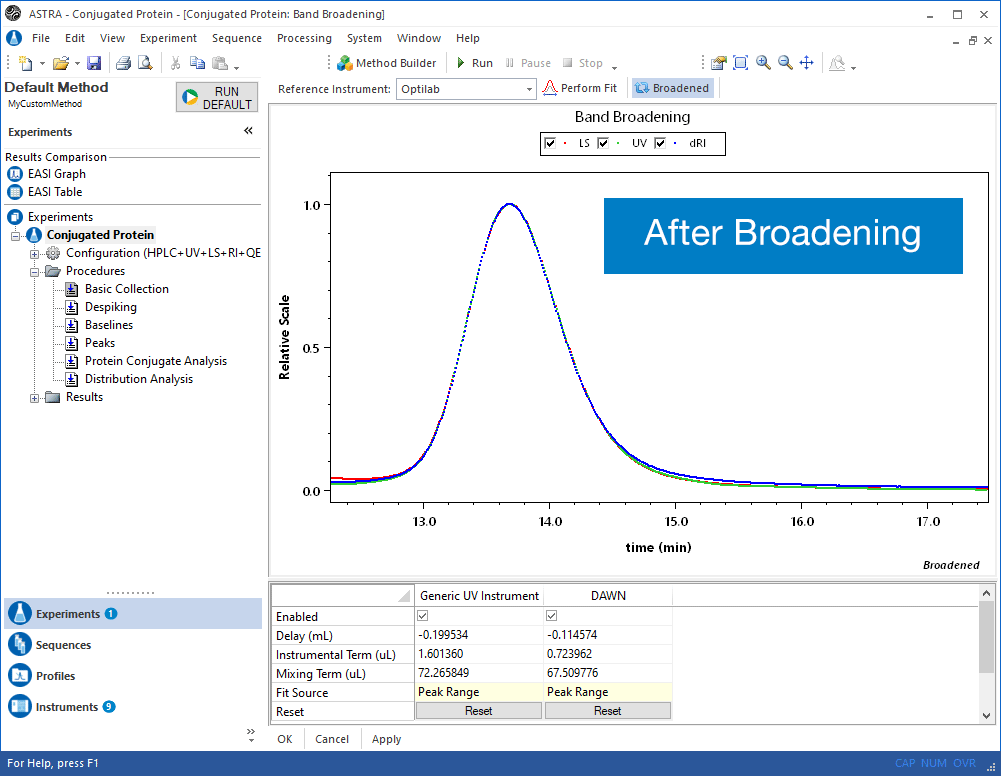
Band Broadening Correction
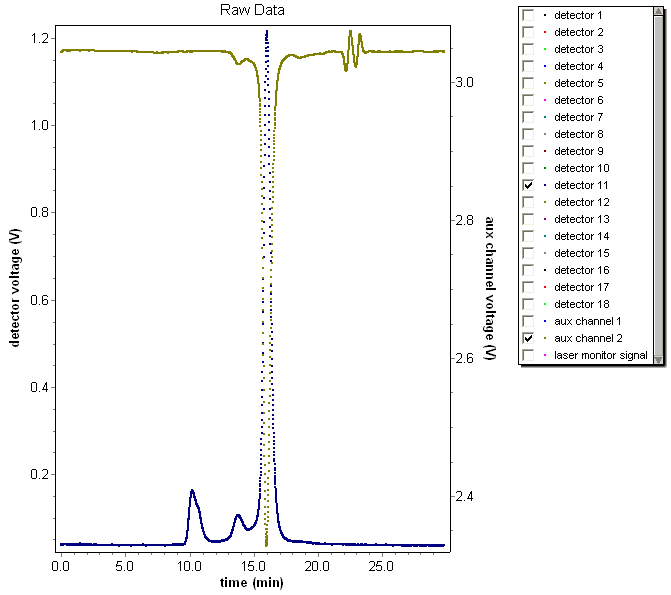
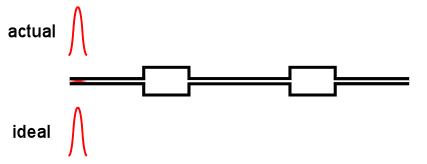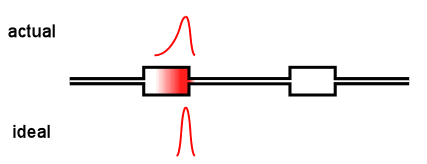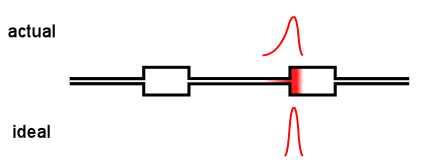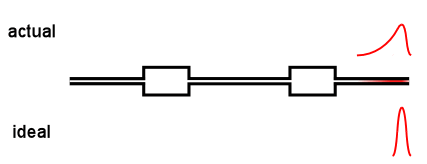 Virtually all online fractionation techniques use detectors in series. As shown in the above animation, however, this creates a fundamental problem. When a narrow "peak" moves along the flow path, each flow cell acts like a small mixing volume that causes the initially sharp peak to broaden with a slight exponential tail. Each detector in the flow path sees an increasingly broadened peak that is different from the initial ideal peak.
Virtually all online fractionation techniques use detectors in series. As shown in the above animation, however, this creates a fundamental problem. When a narrow "peak" moves along the flow path, each flow cell acts like a small mixing volume that causes the initially sharp peak to broaden with a slight exponential tail. Each detector in the flow path sees an increasingly broadened peak that is different from the initial ideal peak.
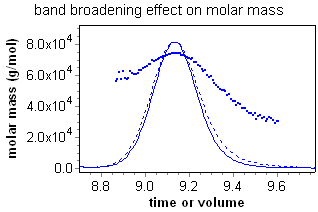 Although this broadening might appear slight, it has deleterious effects on any analysis method that relies on data from multiple detectors. Consider the fractionated BSA monomer sample at right detected by a light scattering (LS) and refractive index (RI) detector in series. The calculated molar mass depends on the ratio of the light scattering and refractive index peaks. The RI peak (dashed line) has clearly been broadened with respect to the LS peak (solid line), resulting in a calculated molar mass that has a "grimace", or frown across the peak. For BSA monomer, however, the mass should be constant across the peak.
Although this broadening might appear slight, it has deleterious effects on any analysis method that relies on data from multiple detectors. Consider the fractionated BSA monomer sample at right detected by a light scattering (LS) and refractive index (RI) detector in series. The calculated molar mass depends on the ratio of the light scattering and refractive index peaks. The RI peak (dashed line) has clearly been broadened with respect to the LS peak (solid line), resulting in a calculated molar mass that has a "grimace", or frown across the peak. For BSA monomer, however, the mass should be constant across the peak.
Wyatt Technology is excited to provide the first real solution to this fundamental problem. Our scientists have developed a patented band broadening correction algorithm that accounts for the physical broadening mechanism. When this band broadening correction is applied, the results are amazing.
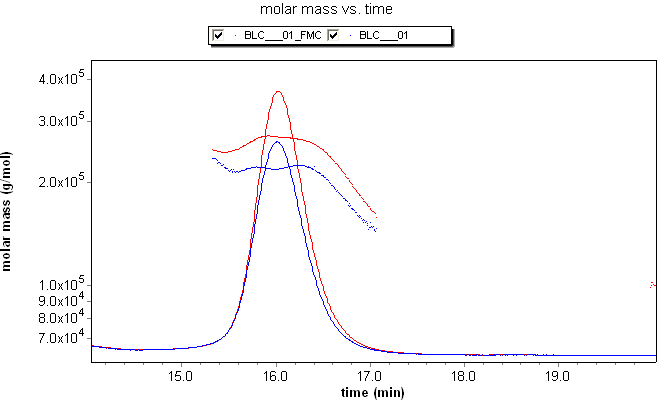
Consider the fractionated BSA series at left, where the data in blue is not corrected for band broadening, while the data in red includes the band broadening correction. The uncorrected data exhibits the classic grimace in molar mass across each peak, while the band-broadening-corrected data clearly shows the "staircase" behavior expected for the oligomer sequence.
The fractionated BSA example also shows the effect of the band broadening correction on the LS trace. Applying the correction modifies the LS trace slightly to match the broadened RI trace. This modification results in little, if any real loss in resolution, yet reveals the molar masses accurately.
The band broadening correction revolutionizes chromatography analysis, revealing trends that were never before visible. Moreover, it is critical for such interesting applications as protein conjugate analysis and viscometry, where three detectors in series are needed, and consequently band broadening effects are even more severe. ASTRA can apply the band broadening correction to an arbitrary number of detectors in series, making it possible to perform even these sophisticated analyses to reveal accurate and exciting new information about your system.
Baseline Correction
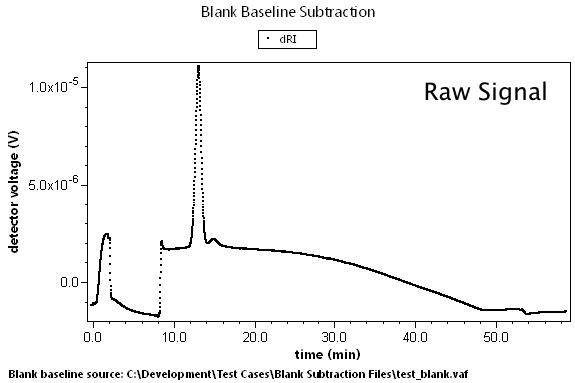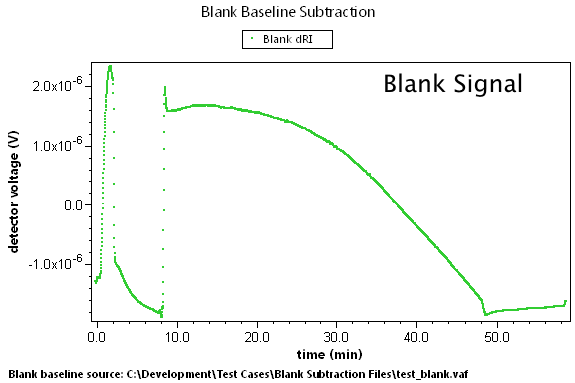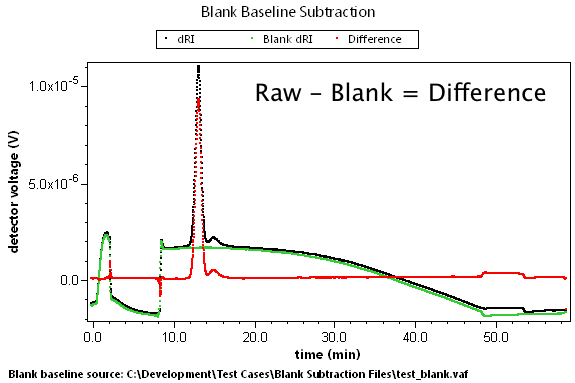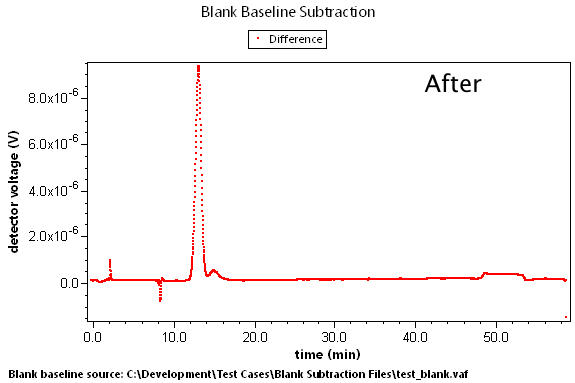
There are many cases where predetermined changes in flow rate, temperature, and other effects can cause instrument baselines to drift such that the standard linear baseline subtraction feature cannot correct for the problem. A set of blank data can be collected that will model these effects. By subtracting this blank run, we can generate well-behaved result data.
Particles and Number Density
In particles mode, it is possible to measure the size and number density of a sample using just a DAWN®. ASTRA supports several sophisticated models to determine the size of a macromolecule based on the angular variation in the light scattering intensity:
- Zimm, Debye, and Berry formalisms: Traditional multipole expansions to determine rms radius of sample regardless of geometry.
- Random coil and sphere: Closed form expressions for particles with known geometries. Applicable in the Rayleigh-Gans-Debye limit where solute and solvent indices of refraction are similar.
- Mie: Full power Mie calculations to determine geometric radius of spherical samples. Applicable to samples with any refractive index.
- Coated sphere: Ideal for modeling lipid vesicles, where thickness of spherical shell is known.
- Rod: If the radius of the rod is known, this model can be applied to determine the length.
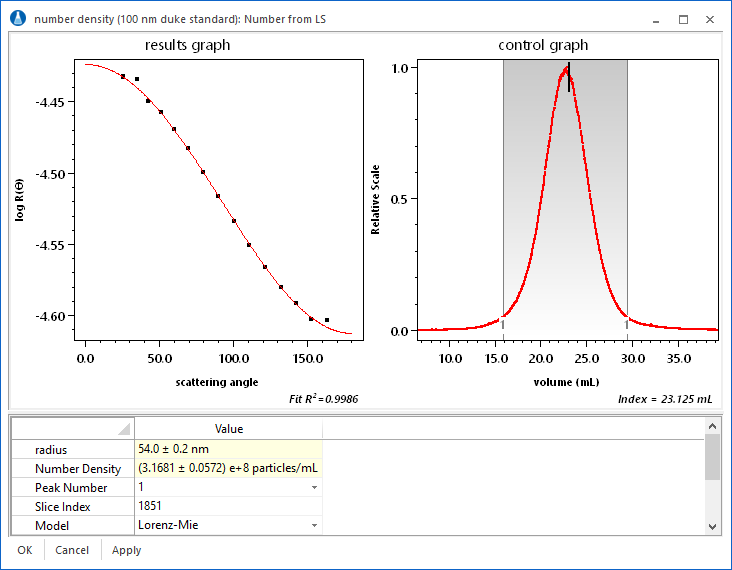
Number Density
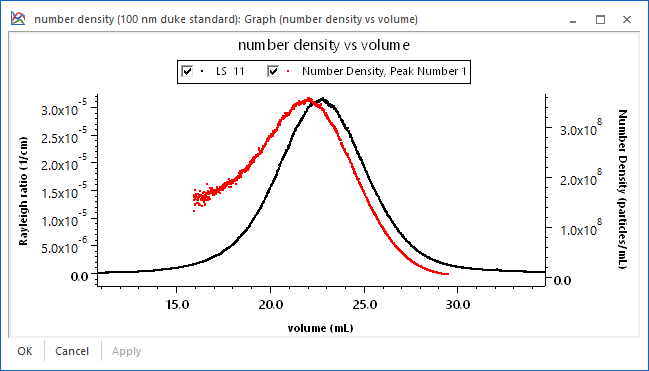
If the index of refraction of the sample is known, it is possible to use ASTRA's proprietary number density calculations. As shown in the screen shot, the geometric radius and number density of a sample are determined for each eluting slice using just a DAWN. The number density calculations make it possible to measure the total number of particles in a peak.
Moreover, using ASTRA's powerful distribution calculations, cumulative and differential number fractions can be reported. For example, the number fraction of a sample between different size ranges can be determined. Finally, it is possible to plot quantities such as absolute number density vs. volume, as shown below for a 100 nm nanosphere sample.
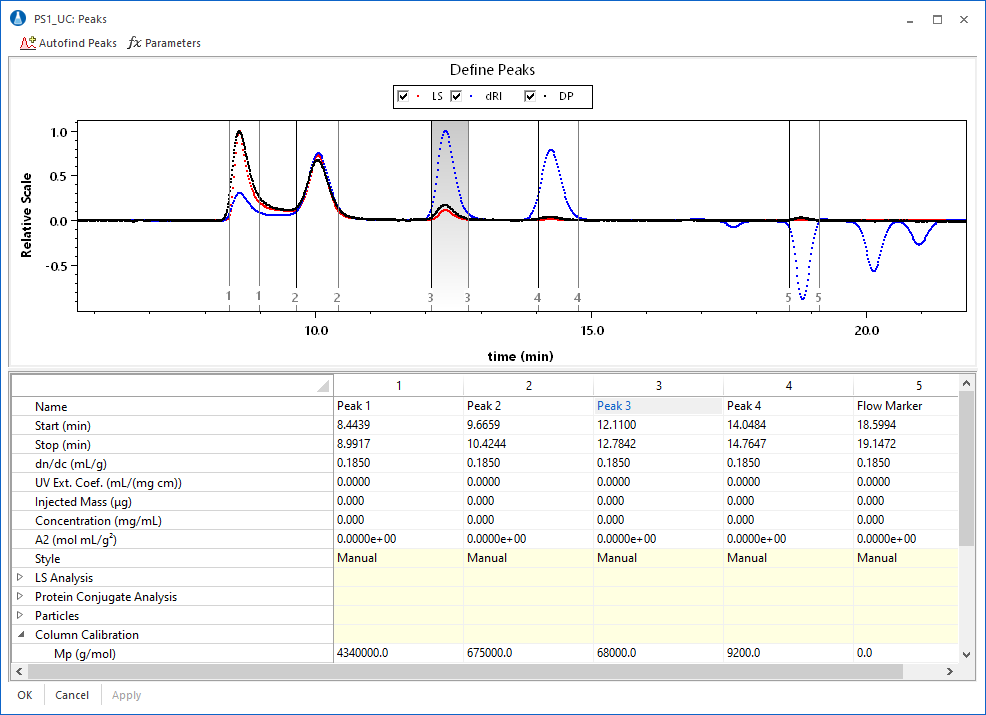
Peak Statistics
Good chromatography has baseline separation between peaks, and peaks should be symmetric. But what if we observe tailing and asymmetry – is the chromatography ‘good enough’? ASTRA can assess the quality of chromatography with statistics such as peak height, column plate count, peak width, asymmetry, tailing and resolution. This analysis is built into every online method in the software so there’s no need for additional chromatography software to perform these calculations.
Visualize these parameters for every in-line detector – MALS, UV or RI – in the customizable ASTRA report.

Error Analysis
Wyatt Technology software is written by scientists for scientists. As a matter of course, we understand that uncertainties in calculated quantities are necessary to evaluate any measurement. All calculated results in ASTRA are presented with rigorous statistical uncertainties, resulting from careful error analysis and propagation of uncertainties.
Moreover, ASTRA contains proprietary algorithms to accurately determine the uncertainty in all measured quantities. These uncertainties are essential for use in further analyses, and for evaluating the signal to noise. When this strong foundation for error analysis is combined with ASTRA's powerful reporting and graphing capabilities, the result is software that gives researchers the tools they need to generate publication quality results with a rock-solid scientific foundation.
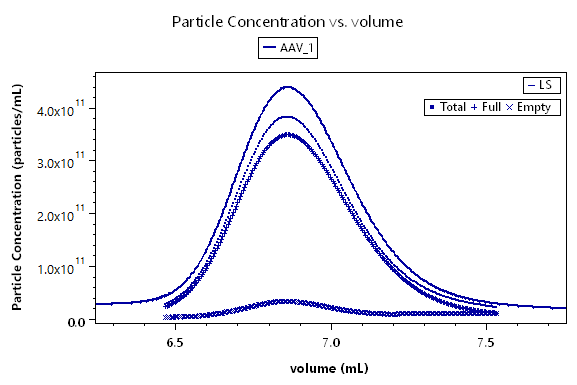
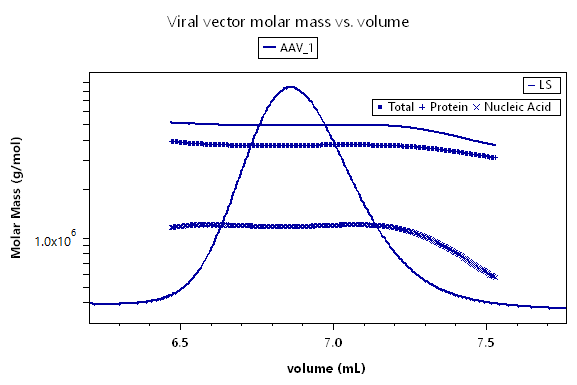
ASTRA’s Viral Vector Analysis determines critical quality attributes including the total number of viral capsid particles, relative capsid content (e.g., ratio of empty and full capsids) and percent aggregates. This analysis works best for smaller vectors such as adeno-associated viruses (AAV) or virus-like particles (VLP), where the impact of scattering on the UV signal is negligible.
SEC-MALS-UV-RI is most often the method of choice for these smaller vectors. FFF-MALS-UV-RI may also be employed, especially if the particles interact with the SEC column or the aggregates are too large for effective SEC separation.
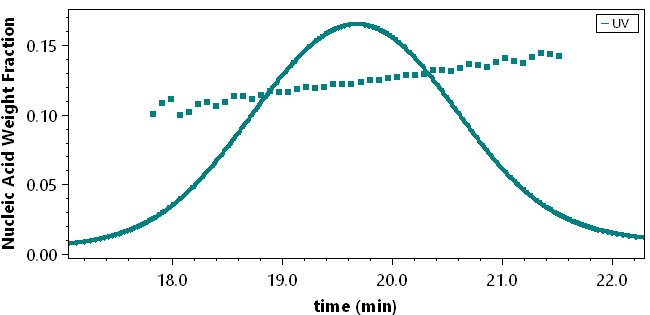
The method requires a MALS detector and two concentration detectors that have differing responses to protein and nucleic acid constituents. Traditionally this is accomplished with the combination of UV and RI. With HPLC CONNECT and its native support for recording digital UV data, the viral vector analysis may also be performed at two different UV wavelengths such as 280 nm and 260 nm.
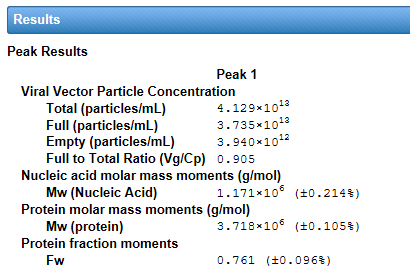
The interface for viral vector analysis is straightforward to use. Enter dn/dc values and UV extinction coefficients, for both protein (capsid) and nucleic acid (genetic payload), to determine total molar mass of the viral particle, molar masses of the protein and nucleic acid components, and the protein weight fraction. Specify the expected molar masses of the protein capsid and full-length nucleic acid as the reference (if they are not known, these parameters can be measured by SEC-MALS), then determine the total, full and empty viral vector particle concentrations, and the capsid to viral genome ratio Cp /Vg.
ASTRA’s EASI Graph feature lets you overlay chromatogram traces and calculated results, such as empty and full particle concentrations or molar masses, from multiple runs. EASI Table compares numerical results from different runs in an easy-to-read format and provides statistical analysis.
Lipid Nanoparticle-Nucleic Acid Analysis
ASTRA’s Lipid Nanoparticle Nucleic Acid (LNP-NA) Analysis provides molar mass and size distributions, polydispersity, payload distributions and encapsulation efficiency from MALS-UV-RI data. The analysis tools are tailored to the quantitation of LNP with nucleic acid (DNA or RNA) payloads.
The method employs a DAWN MALS detector, UV absorption detector (typically at 260 nm) and Optilab differential refractometer. Separation of these particles is usually performed by field-flow fractionation (FFF) using an Eclipse FFF system, but size-exclusion chromatography (SEC) may be suitable as well. An embedded protocol takes you through the analysis step-by-step to ensure consistent processing and data interpretation.
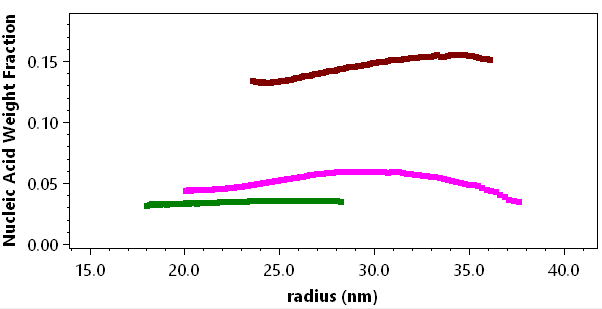
The LNP Analysis module extends ASTRA’s conventional MALS-UV-dRI conjugate analysis to characterization of nanoconjugates such as LNP-RNA. Nanoconjugate analysis is complicated by particle size: whereas macromolecules produce UV signals primarily by absorption, for particles >20 nm in radius, extinction due to scattering by the nanoparticles contributes significantly to the UV chromatogram or fractogram. The scattering effect is evident in the strong UV peak obtained from an empty LNP sample comprising solely non-absorbing lipids. The LNP Analysis module implements a correction for UV scattering which enables correct concentrations from UV absorption and accurate masses of the nucleic acids and lipids (U.S. patent pending).
ASTRA’s EASI graph feature displays various quality attributes, including the unique attribute of payload distribution—the total payload molar mass or relative payload mass, as a function of particle size. These plots help you compare different processes and products, and assess consistency. ASTRA’s EASI table and reports provide quantitative results in a user-customizable view, and facilitate calculation of encapsulation efficiency from the total nucleic acid in the LNP peak.
Molecular Conformation
Light Scattering
When a DAWN or miniDAWN and a concentration detector are used to make molar mass and radius measurements, ASTRA can assess the shape of the molecule based on the measured molar mass and rms radius. A plot of the log of rms radius as a function of the log of the molar mass, called a Conformation Plot, shows the relationship between the two quantities. The slope of this graph gives a good estimate of the shape:
- Sphere: slope is approximately 0.33
- Random Coil: slope is near 0.5 - 0.6
- Rod: slope is approximately 1.0
When molecule sizes are above 10 nm we can measure both molar mass and rms radius simultaneously using only a light scattering instrument and a concentration source.
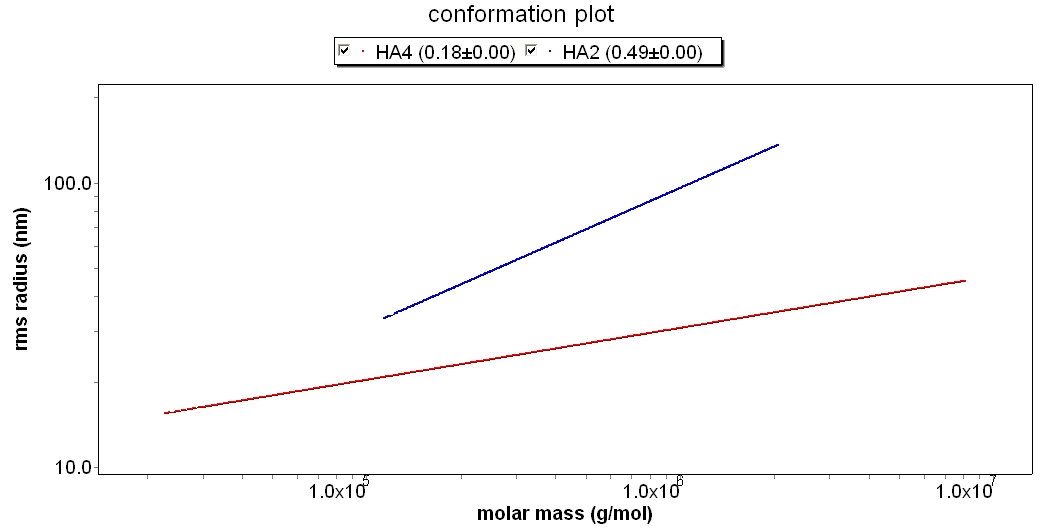
Aqueous Polymer
This conformation plot compares two aqueous polymer samples (hyaluronic acid). HA2 has a slope of 0.49, which indicates that it is a random coil. HA4 has a slope of 0.18, which indicates a much more compact structure. ASTRA's branching analysis could be used with these polymers to assess HA4's highly branched structure more closely.
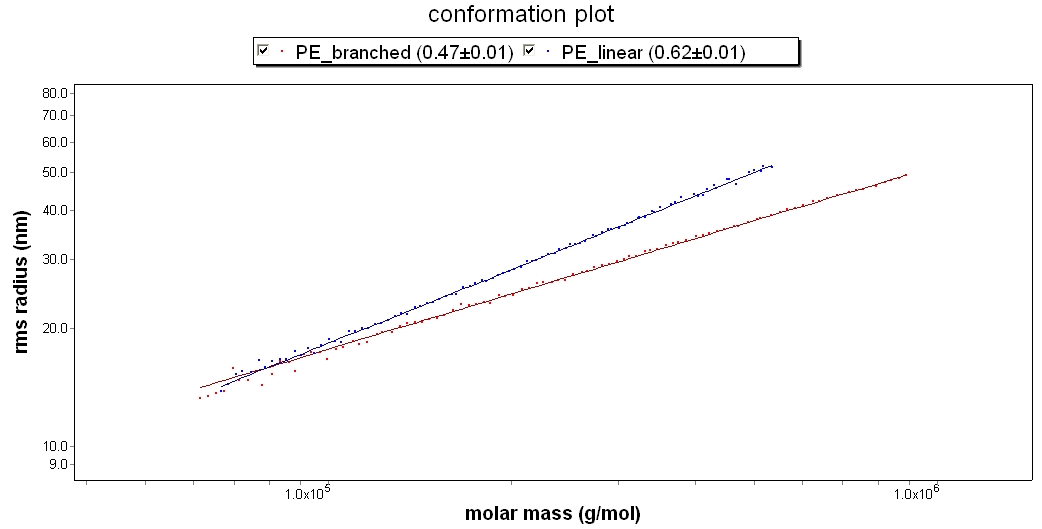
Polyethylene in TCB
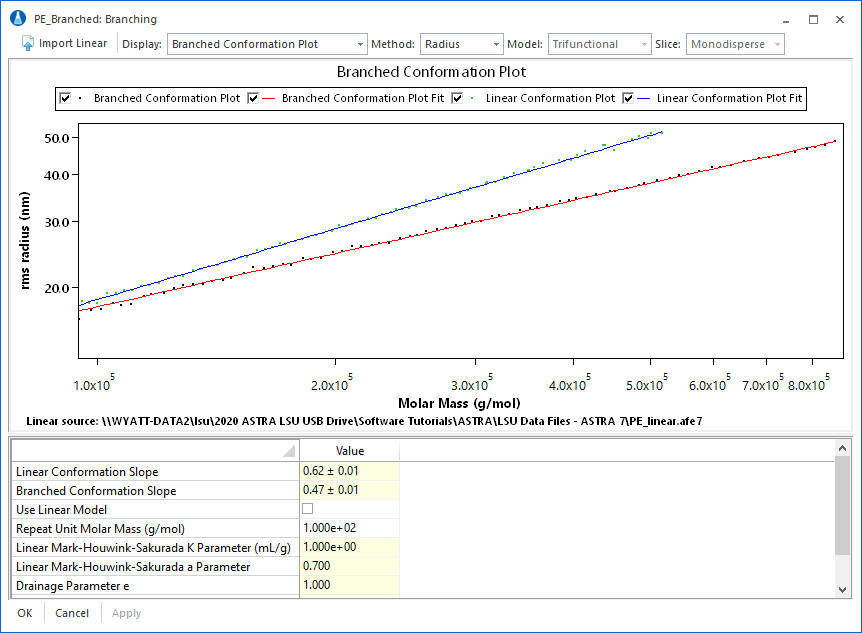
This conformation plot compares two polyethylene samples in TCB at 135°C. PE_linear has a slope of 0.62, which indicates that it is a linear random coil. PE_branched has a slope of 0.47. The difference in slope indicate that the PE_branched sample is more compact, and likely has a more branched structure.
Light Scattering with Viscometry
If we wish to determine the conformation of molecules with rms radius below 10 nm, a ViscoStar can be added to the analysis to determine conformation. A plot of the log of intrinsic viscosity as a function of molar mass, called a Mark-Houwink-Sakurada (MHS) Plot, shows the relationship between the two quantities. As with the Conformation Plot, the slope of this graph (the MHS a term) gives a good estimate of the molecular shape:
- Solid Sphere: a is approximately 0.0
- Linear Random Coil in Theta Conditions: a is approximately 0.5
- Linear Polymers in Good Solvent: a is approximately 0.5 to 0.8
- Rigid Rod: a is approximately 1.8 to 2.0
Aqueous Polymer
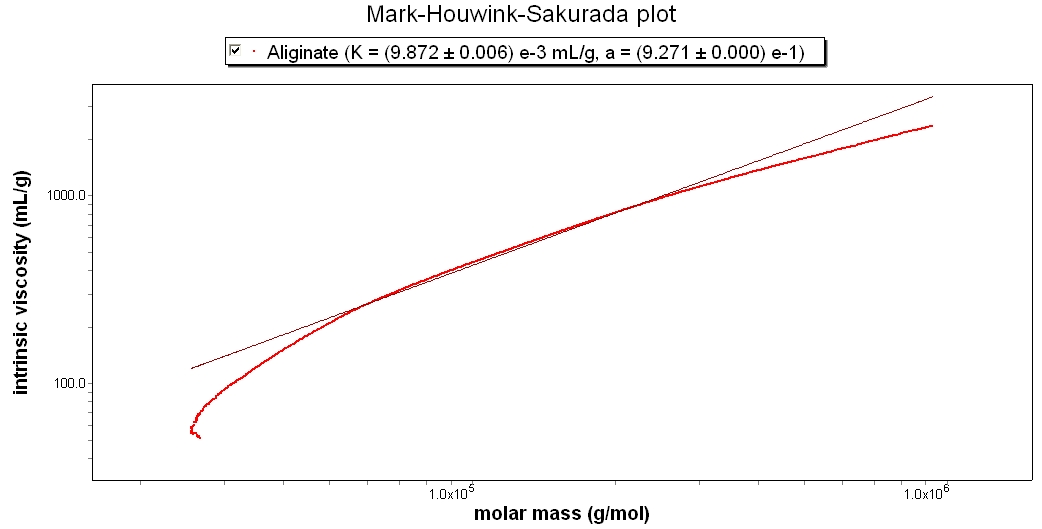
This Mark-Houwink-Sakurada plot shows Alginate, a natural polymer occurring in algae. Its slope is approximately 0.99, which indicates that it is a linear polymer.
Synthetic Polymer
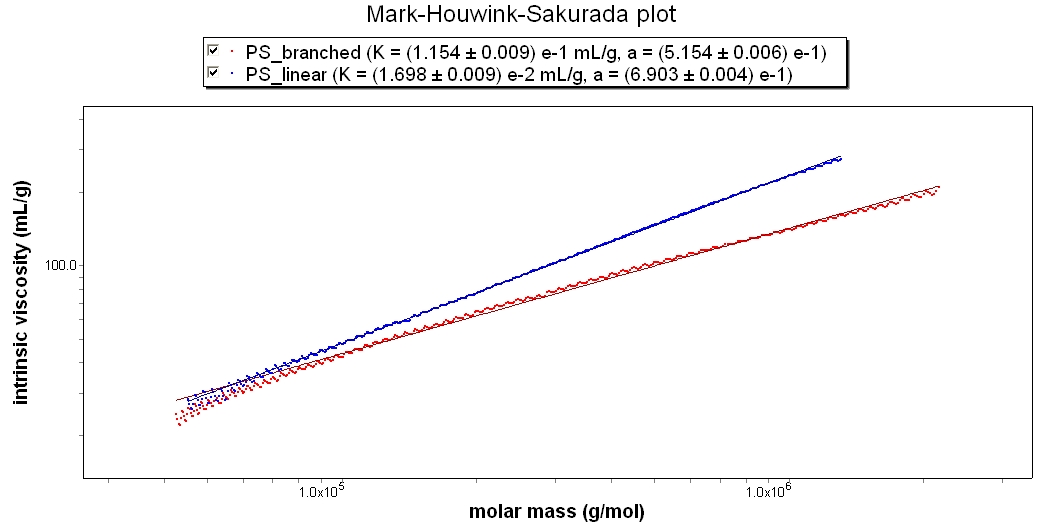
This Mark-Houwink-Sakurada Plot shows two polystyrene samples in THF. The slope of PS_linear is 0.68, while PS_branched is 0.51. While both are random coils, the branched sample is clearly more densely packed.
Branching Calculations
When using a DAWN or miniDAWN to make molar mass measurements, it is possible to perform sophisticated branching calculations to determine the branching of a polymer sample. ASTRA can determine the degree of tri- or tetrafunctional branching, and even analyze star and comb polymers. If the molar mass and rms radius for a linear and corresponding branched polymer are measured, then ASTRA can calculate the following quantities:
- branching ratio gM .
- branch units per molecule.
- long chain branching.
In addition, if the polymer is too small (rms radius < 10 nm) for size measurements using light scattering, ASTRA can use the mass method for samples with known Mark-Houwink-Sakurada parameters and common elution times.
The branching analysis view puts everything at your fingertips to make branching calculations simple. Choose between four different polymer types: tri- or tetra-functional, star, or comb branching. Enter parameters for long chain branching, or the mass method. Finally, instantly view results by selecting the plot type. Displayed at left is the interface with a comparison of conformation plots and slopes for a linear and branched sample.
The following plots demonstrate the other visual information available in the branching analysis view:
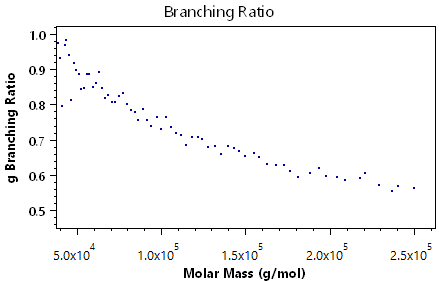
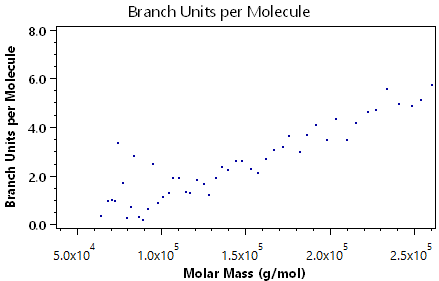
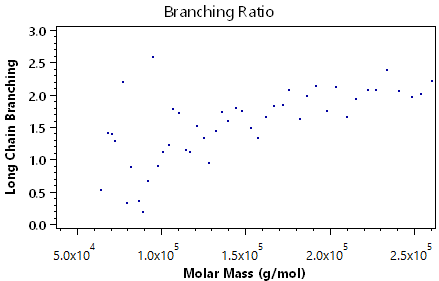
Viscometry
ASTRA has native support for viscometry data collection and analysis from the ViscoStar®. The viscometry module may also be utilized for high temperature GPC applications. Several different types of viscometry analysis are performed. Coupled with Wyatt Technology's experience in measuring molar mass using light scattering, macromolecular characterization via viscometry has reached a new level with ASTRA.
Instrinsic viscosity calculations
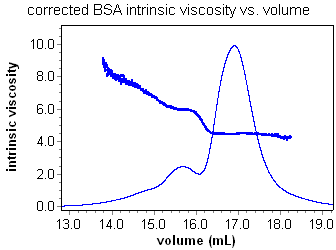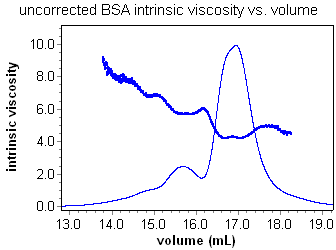
Using the ViscoStar and a concentration detector in series, it is possible to calculate the intrinsic viscosity of a sample as a function of elution volume. Analysis is a snap. Set a peak region and enter a dn/dc or UV extinction value for the sample if using an RI or UV concentration detector respectively. Most important of all, ASTRA's powerful band broadening correction makes accurate analysis of viscometry data possible for the first time. Consider the intrinsic viscosity for a BSA oligomer sequence with and without the band broadening correction. The constant, and accurate, value for the intrinsic viscosity of each oligomer can be determined and reported using ASTRA.
Mark-Houwink-Sakurada plot
Using a combination of the ViscoStar, DAWN or miniDAWN, and a concentration detector, ASTRA can determine the Mark-Houwink-Sakurada constants K and a. The level of accuracy in determining these parameters is unparalled. Coupled with the usual measurement of intrinsic viscosity, the molar masses are measured directly using light scattering. Consider the Mark-Houwink-Sakurada plot for the 706 polystyrene standard. ASTRA provides a new benchmark for determining the Mark-Houwink parameters, and can accurately reveal instances where deviations occur from the classical Mark-Houwink-Sakurada equation behavior.
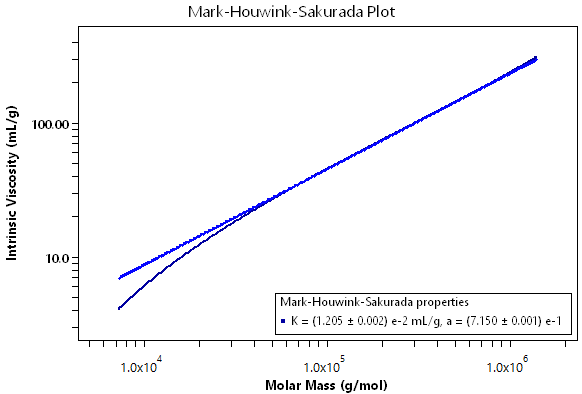
Molar Mass: Mark-Houwink-Sakurada Procedure
ASTRA can take data from the ViscoStar and a concentration detector to calculate the molar mass based on the Mark-Houwink-Sakurada (MHS) equation. To use this procedure, it is only necessary to know the Mark-Houwink K and a coefficients. These can be taken from the literature, or determined with unparalleled accuracy using ASTRA in combination with a light scattering detector, ViscoStar, and concentration detector. Once the molar mass has been calculated, ASTRA's powerful distribution and moment procedures are used to calculate the molar mass moments (Mn, Mw, and Mz) and molar mass distributions for your sample. Most importantly, the MHS procedure benefits from ASTRA's band broadening corrections, making it possible to determine the molar mass accurately for each eluting volume.
Molar Mass: Universal Calibration
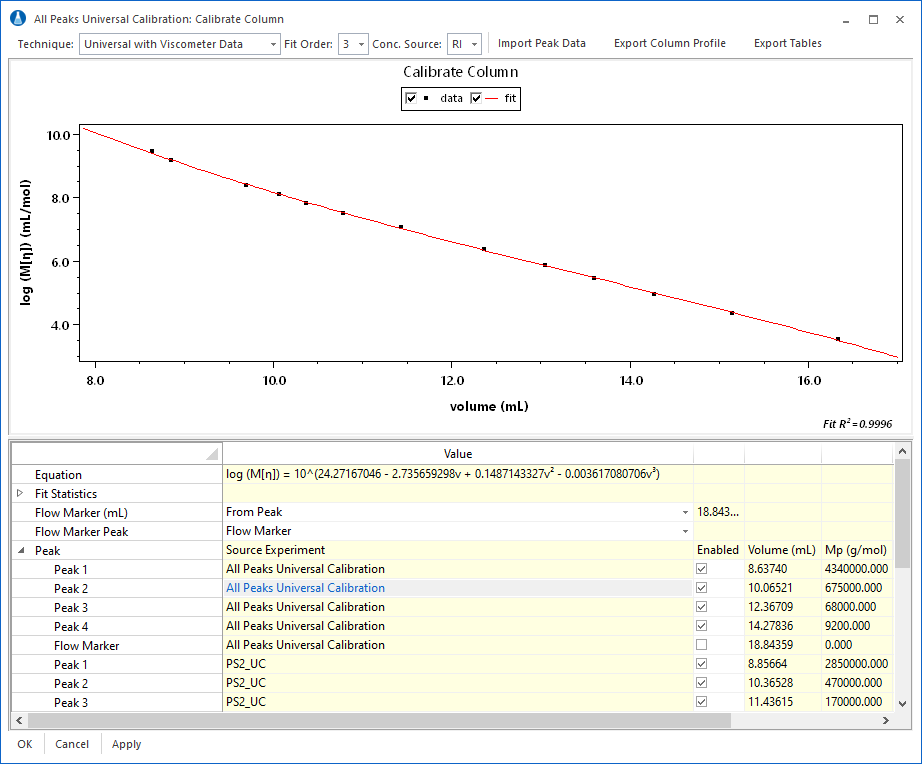
Universal Calibration creates a single calibration curve for a given column using just the ViscoStar and a concentration detector (Optilab or UV). The elution time is directly related to hydrodynamic volume which, in turn, is related to the molar mass and intrinsic viscosity. Assuming the sample is a random coil polymer, intrinsic viscosity and elution time are combined to determine molar mass. Universal Calibration results can be turned into distributions and moments, just like MHS procedure results.
Size calculations
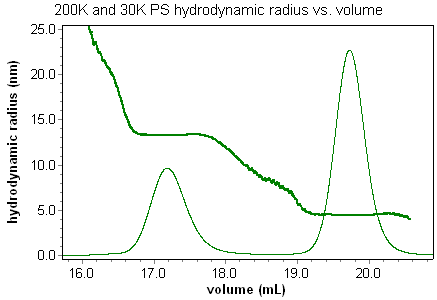
Coupled with the DAWN or miniDAWN and a concentration detector, the ViscoStar can determine an effective size of a macromolecule from its excluded volume. When compared with the rms radius from light scattering measurements, or the QELS hydrodynamic radius, the viscometry size measurements shed new light on macromolecular conformation and properties. Consider the effective size, or hydrodynamic radius, of random coil polystyrene standards in THF. The Rh vs. volume plot shows how well viscometry can determine sizes, and accurately reveal the chromatography of the system. These types of size measurements with viscometry have never been seen before; the band broadening that occurs with a viscometer and two additional detectors is so extreme that only ASTRA's band broadening correction can reveal the true nature of the system.
Distributions and moments
An additional advantage of coupling a viscometer with a light scattering and concentration detector comes from the ability to calculate distributions and moments of the intrinsic viscosity. For example, the traditional number, weight, and z-averaged intrinsic viscosity moments can be calculated for each peak. Also, ASTRA's powerful distribution features make it possible to view accurate plots of cumulative and differential intrinsic viscosity, or the corresponding effective sizes.
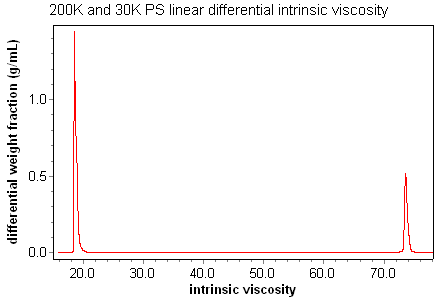
Why the band broadening correction is essential for viscometry
Viscometers have an additional source of broadening beyond mixing (see band broadening correction for details). When a sample enters the second stage of the capillary bridge, it creates a differential pressure that shows up as the viscometer signal. The volume of one arm of the bridge is about 30 µL. Because the sample flow is split in the bridge, the detected elution volume is thus approximately 60 µL for a viscometer. Contrast this with the < 1 µL detection volume of a light scattering or concentration detector.
An initially sharp peak will therefore be broadened by approximately 60 µL for the viscometer alone, without even taking into account the broadening due to mixing. This makes the band broadening correction essential for determining intrinsic viscosity accurately, since intrinsic viscosity is calculated by taking the ratio of the viscometer and concentration peaks.
ASTRA's powerful band broadening correction accounts for the type of broadening present in viscometers, as well as the broadening due to mixing. The results are amazing. For the first time, accurate intrinsic viscosities can be measured for narrow standards.
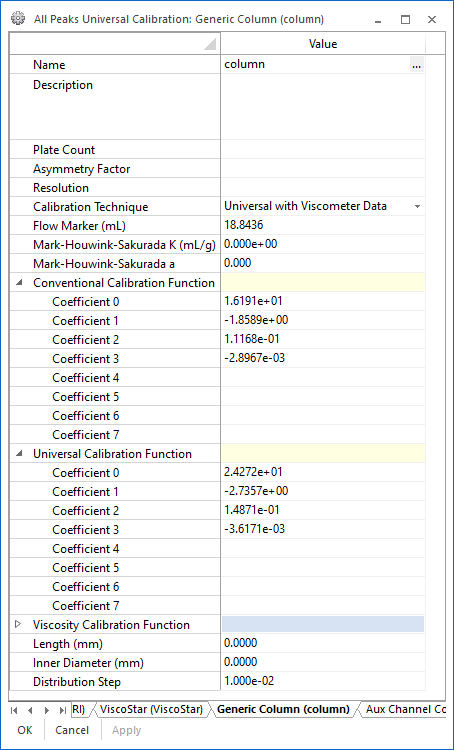
Conventional and Universal Column Calibration
ASTRA supports conventional and universal calibration, allowing chromatographers to build a bridge between their legacy (conventional and universal calibration) data archives, and modern, accurate mass determination through multi-angle light scattering.
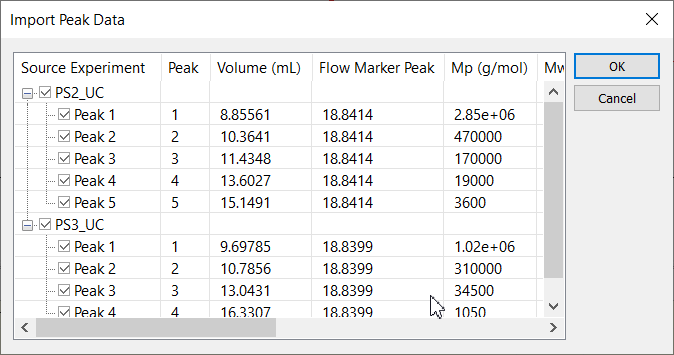
The calibration module includes the ability to merge data from multiple calibration standard runs to determine a column profile across the full column separation range. A typical workflow involves collection of data in multiple sample runs (Figure 1), which are then combined (Figure 2) to form the final calibration curve.
The calibration data from multiple runs can be merged to form a complete conventional calibration curve using the signal of a concentration sensitive detector (typically differential refractometer) or universal calibration curve using either the signal from a concentration detector with Mark-Houwink-Sakurada coefficients, or combined signals from concentration and viscometric detectors.
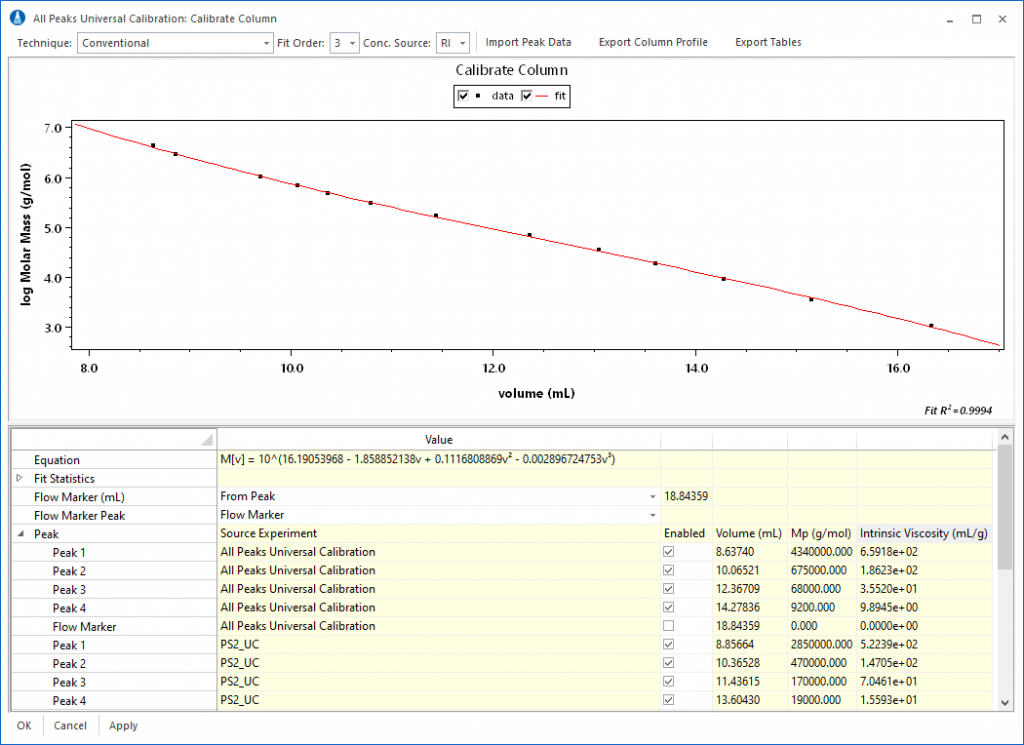
The completed calibration profile can then be used to analyze an unknown sample for average molar mass and molar mass distribution. The calibration results are visible in the column profile, show in in Figure 5, along with fields to hold diagnostic information about the column, such as Plate Count, Asymmetry Factor, Resolution, etc. These fields can be used to track the performance of the column over time.
Comparison of absolute molar mass derived from MALS and relative molar mass derived from calibration results can then be used to build an archive of comparative data mapping absolute to relative molar mass. Comparison of molar masses obtained by conventional calibration with those from MALS can not only illustrate possible errors generated by conventional size exclusion chromatography, but may also be useful for characterization of branching.
On-Line DLS
ASTRA supports data collection and analysis from the WyattQELS DLS Module and certain DynaPro instruments. When analyzing DLS data, ASTRA can:
- Measure the translational diffusion and corresponding hydrodynamic radius of each eluting fraction in an online measurement.
- Determine integral and differential distributions of the translational diffusion coefficients and hydrodynamic radii.
- Calculate the ratio of the hydrodynamic radius (Rh) and rms radius for additional conformation information.
- Present the full correlation function for inspection and analysis.
- Calculate uncertainties in measured quantities.
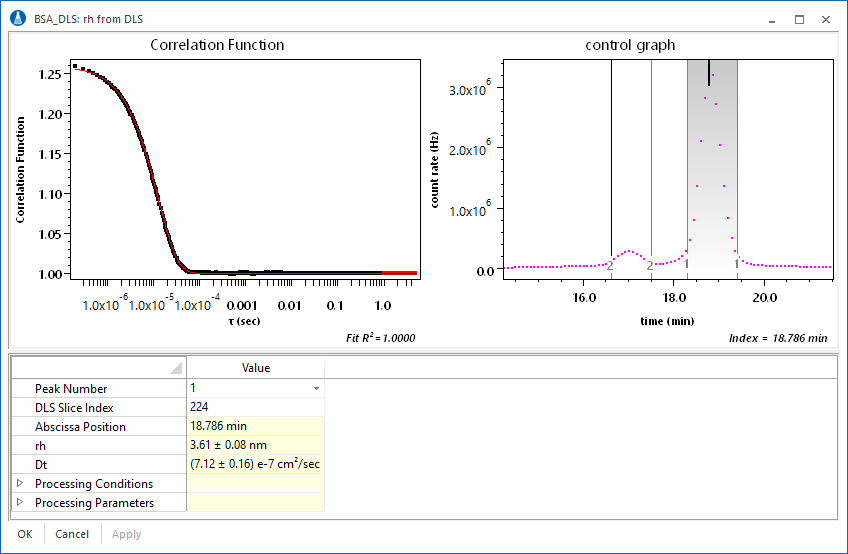
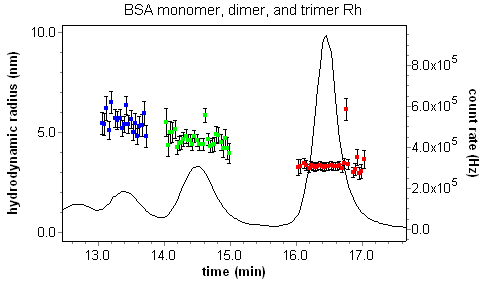
The DLS analysis view in ASTRA presents the correlation function and corresponding single exponential fit. Analysis parameters can be set in the view, with immediate feedback in the results and fit.
Custom plots can be made showing not only the Rh value as a function of elution volume, but also the uncertainties in the presented quantities. Consider the plot of Rh vs. elution volume for a fractionated BSA sequence.
DLS Batch Regularization and Cumulants
As opposed to on-line DLS analysis, batch DLS measurements use the WyattQELS module to characterize unfractionated samples. Batch DLS analysis methods can provide information on the distribution of sizes in a sample.
Regularization analysis
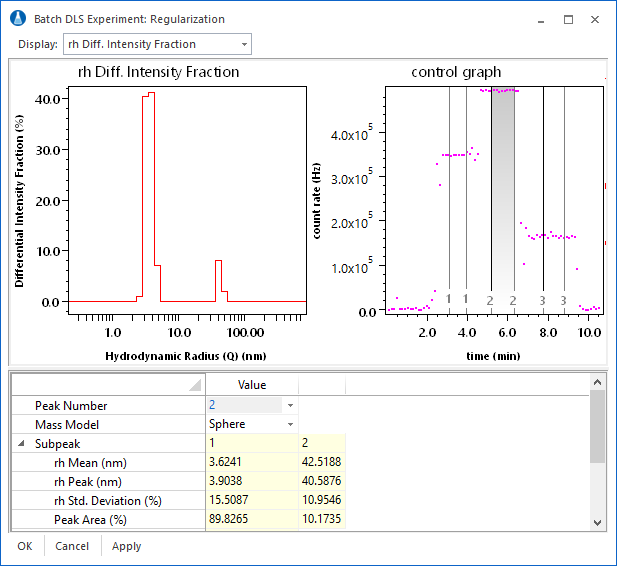
ASTRA uses the sophisticated DYNALS regularization algorithm from ALANGO. DYNALS provides adaptive features along with lightning-fast performance. The DYNALS regularization scheme can be used to determine semi-quantitative distributions for broadly (i.e., over several orders of magnitude) polydisperse samples, and even to resolve two different species in an unfractionated sample if the size difference is at least a factor of five.
The DYNALS regularization analysis is fully integrated into ASTRA. As shown in the experiment at right, baselines and peaks are set as usual, with the regularization analysis as part of the experiment method. Results include hydrodynamic radius (Rh) and translational diffusion (Dt) intensity distributions, and Rh weight distributions based on an assumed sphere or random coil model. The report also contains information on the peaks in the distribution.
The interface for the regularization procedure brings together all of the relevant analysis parameters and results into one view. Changes to the analysis parameters result in immediate feedback from graphs and numerical information.
Features:
- Average of correlation functions over a region to enhance signal to noise.
- Suppression of distribution peaks below a user-defined size.
- Display can be toggled between Rh and Dt distributions or correlation function and fit.
- Conversion from intensity to weight distributions based on either sphere or random coil model.
- Fully 21 CFR Part 11 compliant with ASTRA Security Pack tier.
Cumulants
An alternative analysis technique for characterizing DLS batch Gaussian form, defined by a mean radius and width (polydispersity), indicative of the homogeneity of the population. This is referred to as the Cumulants fit. These results are presented in real time, in numerical and graphical form.
Features:
- Average of correlation functions over a region to enhance signal to noise.
- Pre-filtering of correlation functions based on single exponential fit.
- Correlation function fit and residuals can be displayed.
- Graphical display of range of one standard deviation showing mean and range of sizes for each aquisition.
- Fully 21 CFR Part 11 compliant with ASTRA Security Pack tier.
Data Safety, Integrity & Validation
21 CFR Part 11 requires that electronic data be persistent, and that any changes to the data be recorded in an audit trail. ASTRA and DYNAMICS employ three methods to ensure this:
- All data and audit trails generated by ASTRA and DYNAMICS under Security Pack mode are stored in a secure, ODBC-compliant database. The database can be networked for automatic back-up by the IT department. This ensures that data will not be lost, and that any changes to the data will be associated with an audit trail in the same database.
- Encrypted checksums: Each entry in the database has an encrypted checksum. ASTRA and DYNAMICS use this checksum to verify that the data being read from the database has not changed since it was last written, and notify the user of any data corruption or any attempt to alter the data.
- Results comparison: (ASTRA only) ASTRA stores computed results in the database. Each time the data are reprocessed through ASTRA the results are compared against the historical version in the database. If the results change, ASTRA notifies the user so that appropriate action can be taken. This feature can be extremely helpful in validating software updates or new installations.
Validation
Incoming Qualification and Operational Qualification documents are provided with ASTRA and DYNAMICS Security Packs, ensuring validation at the lab site.
In addition, both ASTRA and DYNAMICS are completely validated products:
- All software development is done under a formal quality system, using a standard software lifecycle model.
- Documented testing and traceability is performed to demonstrate accuracy, reliability, and consistent intended performance.
- The ability to discern altered or invalid records is built in.
We welcome audits of the software development and maintenance process by customers' qualified auditors.
User Security
In a compliant installation, system access is limited to authorized individuals. Wyatt software leverages the Microsoft Windows security system to provide user authentication:
- Secure login - In order to run ASTRA or DYNAMICS with Security Pack enabled, users must enter a unique user ID and password. Logins, login attempts, and logouts are all recorded in the system audit trail.
- Microsoft Windows user accounts and groups are leveraged for security. System administrators create four specific security groups, then associate existing Microsoft Windows users with these groups. The Microsoft Windows user accounts are then used to log in.
- It is possible to set up the ASTRA or DYNAMICS security groups in the Active Directory, such that network-authenticated accounts can be given appropriate privileges. One domain-level user account can then be used to log in to any instance of ASTRA or DYNAMICS on the network.
Privilege levels
User accounts can have one of four privilege levels:
- Administrator - Administrators have rights to perform all actions, including changing database connections and deleting data.
- Researcher - Researchers can create and run new methods, change instrument configuration settings, and export and import data from the database.
- Technician - Technicians can only run predefined methods set up by a Researcher. Technicians can collect data and perform simple processing, but cannot change any configuration settings.
- Guest - Guests have read-only privileges to view audit trails and data.
Audit Trails
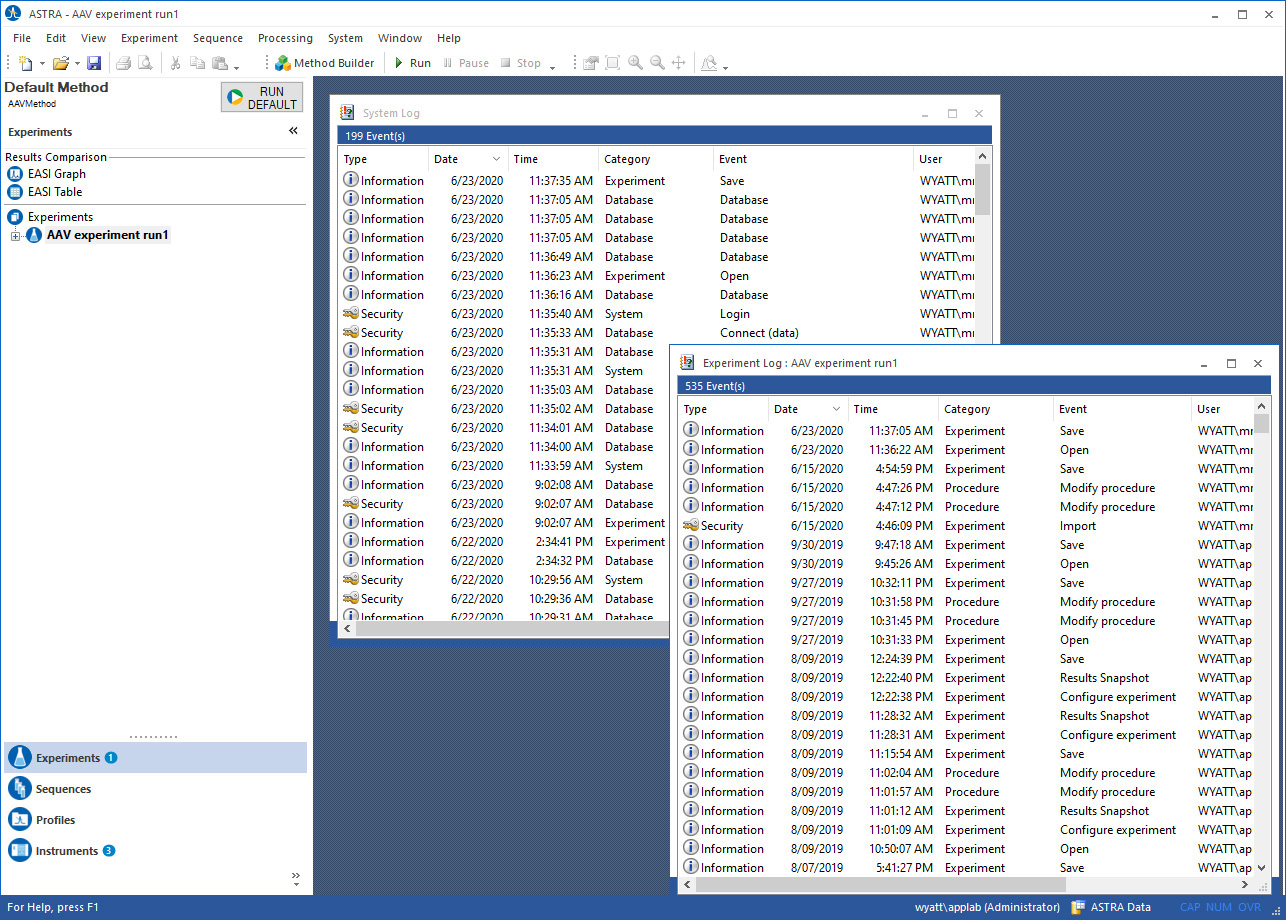
ASTRA and DYNAMICS provide two levels of audit trail to independently record all operator actions that create, modify, or delete electronic records. Each entry in the audit trail is time-stamped, and records the operator performing the actions, as well as the computer where the actions are performed. In the screen shot on the right, the general view of the system log is displayed, along with an experiment log.
System log
The system log is always associated with the database where the data is stored. This audit trail cannot be separated from the data associated with it. The system log records actions such as:
- Logins, login attempts, and logouts
- Data creation, modification, and deletion
- Database connections and disconnections
- Import and export of data from the database
Experiment log
Each experiment has a separate log that records all actions within the experiment that affect the data. The experiment log is always with the experiment, and cannot be reset. The experiment log records actions such as:
- Changes to instrument configuration settings
- Changes to analysis methods
- Collection of data
- Electronic signatures executed to the experiment
- Changes in presentation methods
Electronic Signatures
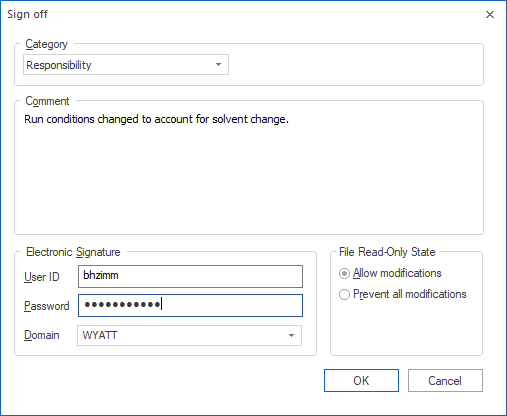
Electronic signatures can be executed on any data collected in ASTRA or DYNAMICS under Security Pack mode. To perform an electronic signature, the user first specifies a signature meaning (such as responsibility, approval, or review) and description, then enters a unique user ID and password. The electronic signature is executed to the experiment log associated with the data, and shows up in the report associated with the experiment.
Multiple electronic signatures can be executed to an experiment. In the reported results, the software flags any electronic signatures that were made before the last modification. Failed electronic signature attempts are recorded in the system log with an alarm status for immediate notification of system administrators.
Enforcing Permitted Sequences
Ideally, a 21 CFR Part 11 compliant application should be usable for quality assurance in a manufacturing process. To meet this goal, it is necessary that the application support "operational system checks to enforce permitted sequencing of steps and events". In other words, it should be possible for a technician in quality assurance to run the application with minimal input and limited possibility to affect the results through incorrect decisions.
ASTRA and DYNAMICS SP have strong support for enforcing permitted sequences through the methods (known as 'presets' in DYNAMICS). A user with Researcher privilege level can create a new experiment, and then save it as a Method. A user with Technician privilege level can only use the Method to collect and analyze data, and cannot make changes to the Method configuration, analysis, or results reporting.
With their template/preset technology, ASTRA and DYNAMICS support moving macromolecular and nanoparticle characterization into everyday manufacturing and quality assurance applications.
Human Readable Records
All of the data that ASTRA and DYNAMICS generate are made available to the user in human readable form. Using powerful data export and presentation capabilities, all data can graphed, shown in tables, or exported to text. In addition, ASTRA reports are customizable to present the data of interest, and can be exported to PDF or HTML format.