多角度静态光散射理论
在19世纪,第三代瑞利男爵 (约翰·斯特拉特) 首次解释了天空明亮的蓝色。 他的见识基于理论物理学的最重要的成就之一: 詹姆斯·克拉克·麦克斯韦于1865年提出的描述光和其与物质的相互作用的基本方程式。以伸展瑞利男爵的理论,可以形容光如何被溶液中大分子散射。这称为瑞利-甘斯-德拜(Rayleigh-Gans-Debye)光散射理论。
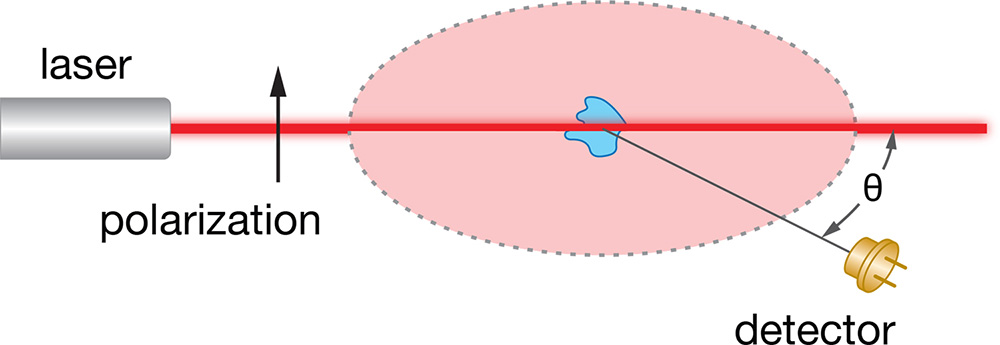
在一个典型的光散射实验中,利用一束准直的单频偏振光(即激光)照射对象,即大分子或纳米颗粒悬浮液。偏振光束的电场最好垂直于测量所散射的光的强度和角度依赖性的平面 (按照惯例,偏振方向称为"垂直",测量平面称为"水平")。总强度携带关于摩尔质量的信息,而水平平面中的角度依赖性携带关于大分子尺寸的信息。
以下理论部分介绍少许关于多角度光散射的专题:

强度和摩尔质量
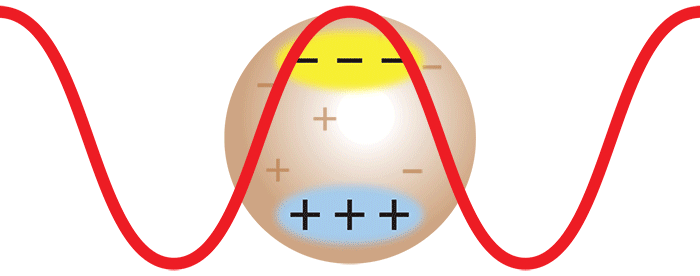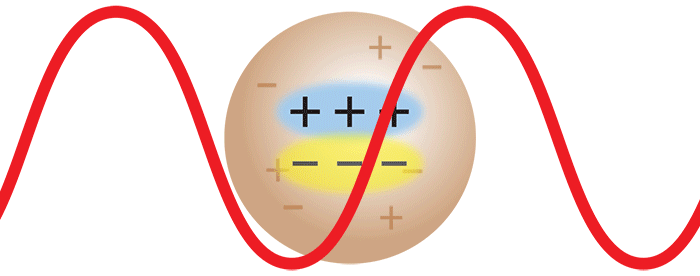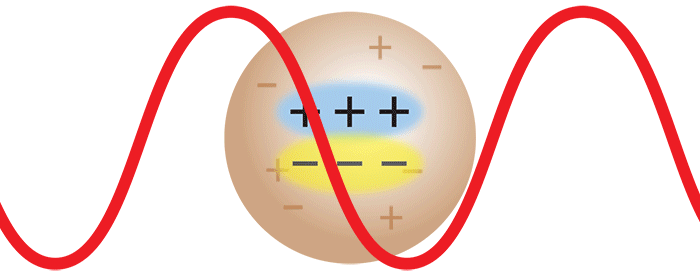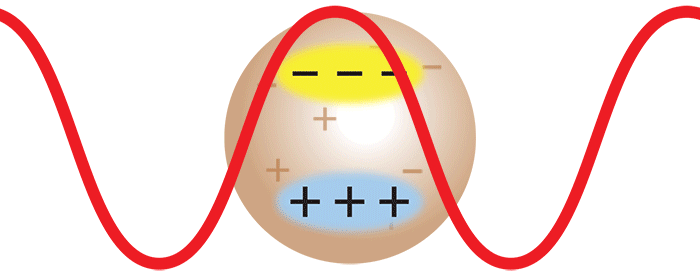
当激光撞击大分子时,光的振荡电场会导致其内部产生一个振荡偶极子。这个振荡偶极子将重新散发出光,就像无线电台的天线发出无线电波一样。辐射光的强度取决于大分子中感应的偶极子的大小。大分子的极化程度越高,感应的偶极子越大,因此散射光的强度越大。因此,为了分析这种大分子溶液的散射情况,必须知道它们相对于周围介质(即溶剂)的极化率。这可以通过使用Optilab®示差折光仪测量dn / dc(=Δn/Δc)值,通过测量溶液的折射率的变化Δn与分子浓度变化Δc来确定。
当溶液中有许多大分子时,每个大分子都会通过上述诱导的偶极子机制散射光。因此,散射光的强度与溶液中大分子的浓度成正比。例如:两倍的分子将会散射两倍的光。
现在考虑其他情况,两种单体在溶液中聚集形成二聚体。最初分离的单体经常受到溶剂分子的碰撞,并经历称为布朗运动的随机运动。这赋予了散射光的相位随机性,使得来自两种单独单体的光是非相干的。随时间平均,散射强度如经典所预期的那样相加:1 +1 = 2。
然而,一旦单体形成二聚体,则两种单体一起移动。现在,来自一种单体的散射光与来自另一单体的散射光具有确定的相位关系。换句话说,散射是相干的。最终结果是,来自二聚体的散射光的强度是来自两个独立单体的总散射光的两倍。简单来说,摩尔质量增加一倍,在保持质量体积浓度相同的情况下,散射光的强度也会加倍。借助 DAWN® 或 miniDAWN® 多角度光散射检测器测得的分子散射光的强度与摩尔质量成正比。因此,光散射代表了一种强大的技术,可用于确定溶液中大分子的摩尔质量以及监视聚集体的存在和形成。
角度依赖性和尺寸
可以将远小于入射光波长的大分子看做本质上是点散射体。对于这种非常小的分子,散射到水平面方向中的光与散射角无关---每个散射角都是相同的,各向同性光散射。
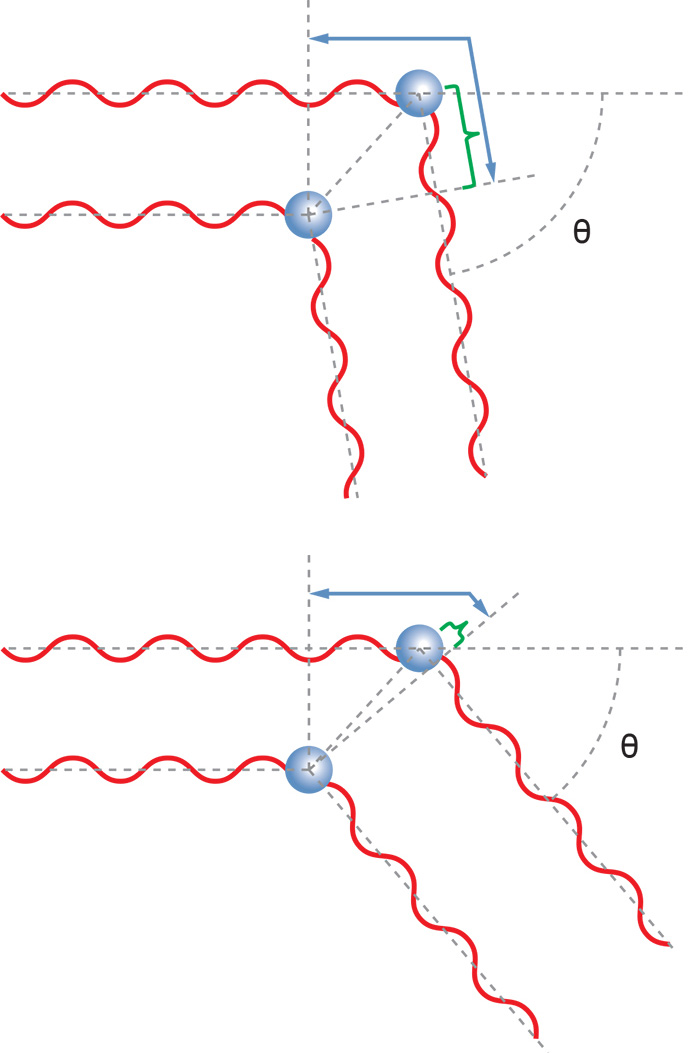
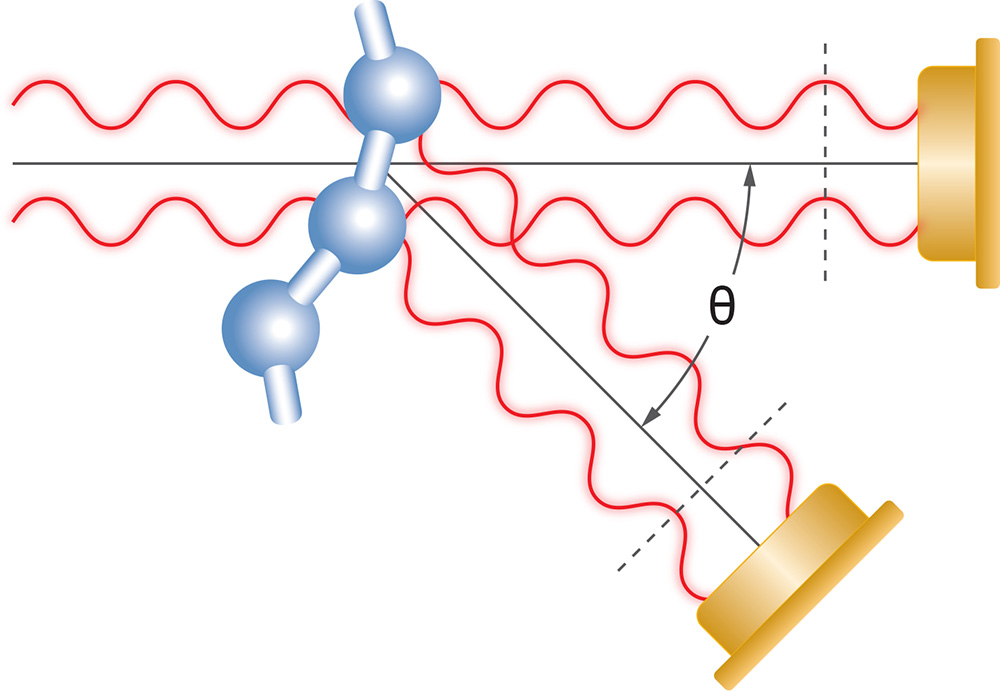
对于较大的大分子,从大分子不同部分散射的光以不同的相位到达探头,这可能导致检测器上整个光波的相消或相叠加的。分子间的干涉现象会导致散射信号随观测角度变化而变化。0角度无光强度的衰减;随着观测角度的增加,散射光强度的衰减也增加。前面提到的RGD理论描述了这种情况。
如果在水平面上测量散射光的角度依赖性,则可以确定分子的大小。这种尺寸测量称为均方根(rms)半径,有时也称为“回转半径” Rg。均方根半径是分子大小的度量,该大小由围绕其质心的质量分布加权。如果确定分子的构象属于特定类别(例如,随机线圈,球形或杆形),则有效值半径可以与其几何尺寸相关。可以通过SEC或GPC分离分子量分布较广的样品,并在每个洗脱体积处获取光散射数据,以确定摩尔质量Mw和Rg。可以将测得的均方根半径与相应测得的摩尔质量作图,以确定样品的构象。
颗粒浓度
利用散射光的角度依赖性和总散射强度来确定尺寸,可以测量另一个重要特性:纳米颗粒的浓度N。
计算需要粒子的体积V和折射率nparticle,以及溶剂的折射率n0。需要假设特定形状,如球体或杆。然后,与形状相对应的方程可适合于角度数据,以获得诸如半径或长度之类的尺寸,由此计算粒子的体积。粒子组成材料的折射率可在文献中找到。为了评估颗粒浓度,必须将角度数据外推至角度零。
如果粒子不由均质材料组成,则使用的折射率值应为粒子整个体积的重量平均折射率nw。例如,包膜病毒的nparticle将是蛋白质、核酸和聚糖的n值的重量平均值。对于空脂质体,应考虑核心中的溶剂含量。
要了解更多信息,请访问粒子浓度页面。
方程和数据分析
Bruno Zimm1所奠定的理论基础使Rayleigh-Debye-Gans光散射理论的结果更有可能凝聚成一个简单方程。正如Philip Wyatt在1993年2的评论文章中所述,Zimm的发展导致了以下方程:
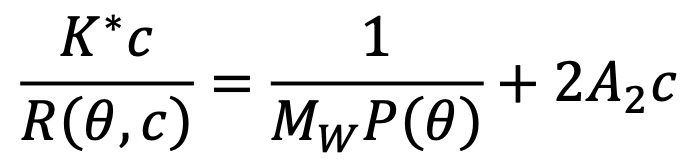
这个公式中:
- R(θ,c) 是溶液的过量瑞利比,表示为散射角 θ 和浓度c的函数。它与散射光的强度成正比,散射光即纯溶剂散射光之外。
- c 是溶质浓度。
- Mw是重均溶质摩尔质量。
- A2 是渗透压维里膨胀的第二维里系数。
- K* 是常数 4π2(dn/dc)2n02/Naλ04.
- Na 是Avogadro常数。以g/mol为单位测量摩尔质量时,始终会出现该数字。
- P(θ) 描述了散射光的角度依赖性,且与均方根半径有关。
P(θ)扩展到一阶得到:
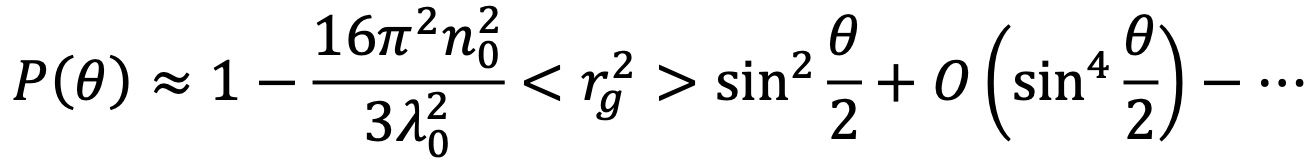
其中 n0是溶剂的折射率,λ0是激光器的真空波长,Rg是均方根半径。在这里,散射光的大小和角度依赖性之间的关系是清楚的。对于较大的颗粒(Rg 大于约50 nm),必须在P(θ)的膨胀中包含更高的矩。
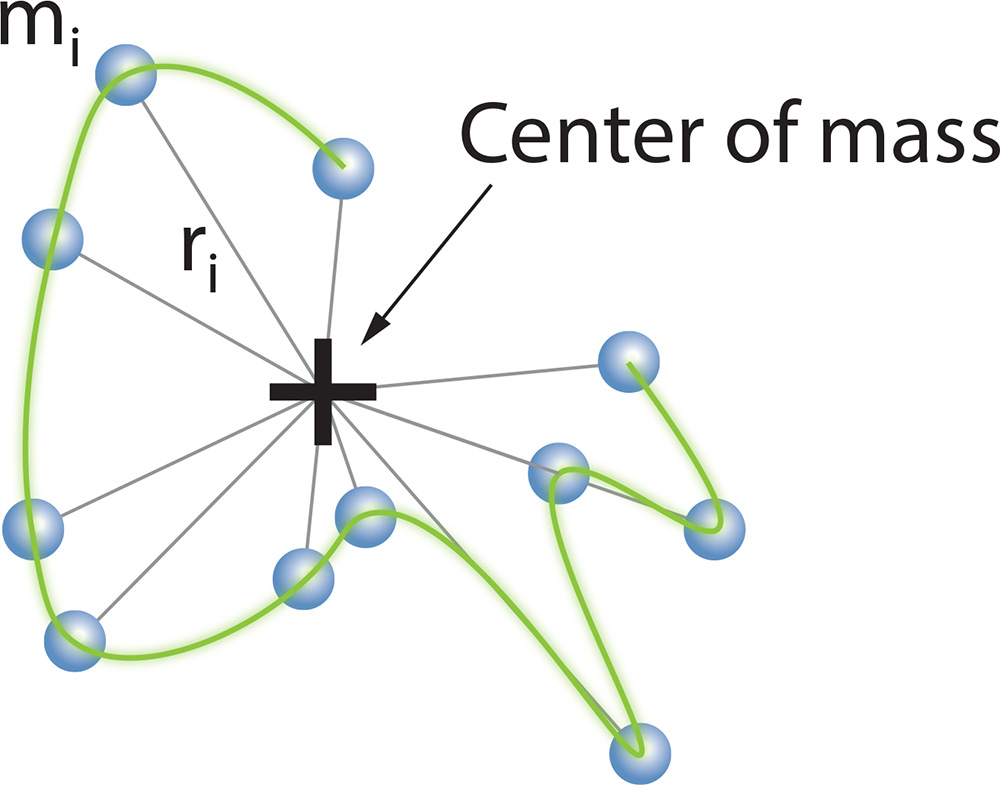
均方半径<rg2>可立即从测量比值 1/R(θ,c) 相对于 sin2(θ/2)的θ = 0 处的斜率计算。如果质量M 的大分子是由mi元素构成的,则可以证明下面的方程:
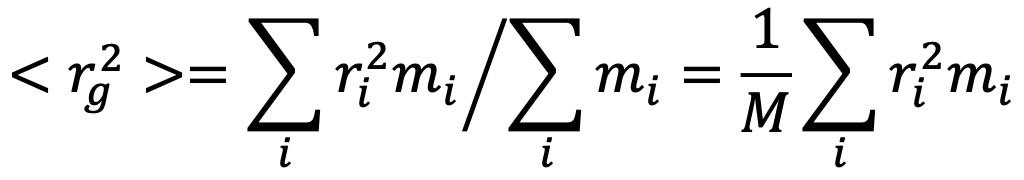
方程式中,ri 是元素 mi与总质量M分子质量中心的距离。
基本的光散射方程在所有角度都成立,而不仅仅是一个!利用现代计算机,我们收集所有角度数据并应用全局拟合,因为质量、尺寸和测量量之间的关系在所有角度都是有效的。所谓的“外推”(一些光散射供应商可能会提到)实际上包括收集一组完整的独立数据点,并使用散射模式的全视图来找到摩尔质量、尺寸和构象的最精确值。因此,Wyatt 的18角 DAWN 同时进行了18次测量。
将从多角度获得的数据结合起来,意味着大大提高了精度和精确度。然而,有些人会争辩说,在一个单一的低角度范围测量(事实上,可能是噪音最高的位置!)优于在一定角度范围内的测量。显然,这个论点是不正确的,这一点可以通过控制方程得到证实。
References
1 Zimm, B. H. The scattering of light and the radial distribution function of high polymer solutions. Journal of Chemical Physics 16, 1093-1099 Ibid. Apparatus and methods for measurement and interpretation of the angular variation of light scattering; Preliminary results on polystyrene solutions. Journal of Chemical Physics 1948, 16, 1099-1116.
2 Wyatt, P. J. Light scattering and the absolute characterization of macromolecules. Analytica Chimica Acta 1993, 272, 1–40.
