动态光散射理论
在溶液中时，大分子会受溶剂分子的冲击，这导致分子的随机运动，其称为布朗运动。例如，考虑在纯水中2微米直径颗粒的图片。可以看出，每个粒子都在不断移动，并且其运动与其他粒子无关。 （图片由Emory University Dr. Eric R. Weeks提供）。
布朗运动
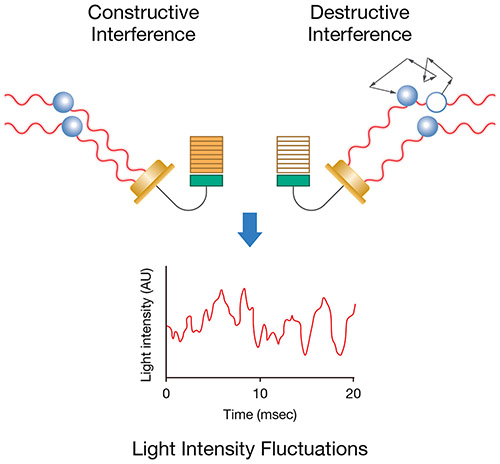
当光从运动的大分子之间散射时，这种运动使散射光的相位具有随机性，因此当来自两个或多个以上粒子的散射光相加时，将会产生相干光和非相干光。这会导致散射光强度随时间的波动。（图1）
在动态光散射（DLS）中，散射光的时间相关波动由单个光子计数模块测量。波动率与分子通过溶剂的扩散率直接相关，而后者又与粒子的流体动力学半径相关。较小的粒子扩散得更快，导致波动强度比较大的粒子更大。因此，光强度的波动包含有关分子扩散的信息，可用于提取扩散系数和计算颗粒尺寸。
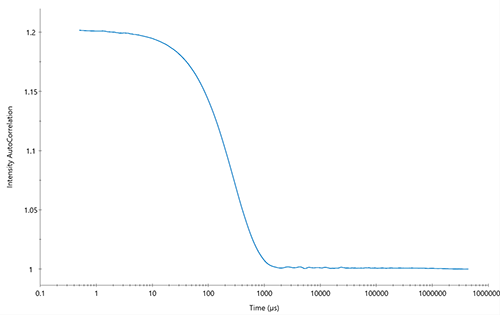
DynaPro® NanoStar®，DynaPro® Plate Reader，Mobius™ 和 WyattQELS™ 模块采用 DLS 来确定 MALS 检测器的有效粒径。分析物的平移扩散系数 Dt 是通过自相关函数的自动非线性最小二乘拟合获得的，该函数定量地描述了光散射强度随时间的测量波动。分析直接在随附的 DYNAMICS®，DYNAMICS® Touch™ 或 ASTRA® 软件中完成。单分散样品的典型自相关函数如图 2 所示。
斯托克斯-爱因斯坦方程给出对应于测量的 Rh 的流体动力学半径 Dt （图 3）：
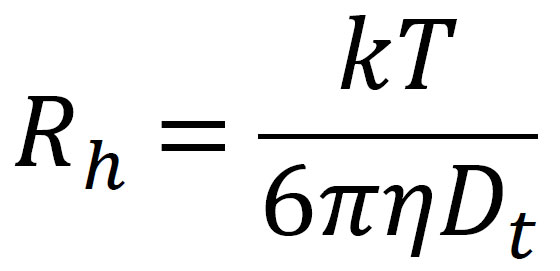
其中 k 是玻尔兹曼常数，T 是以 K 为单位的温度，h 是溶剂粘度。
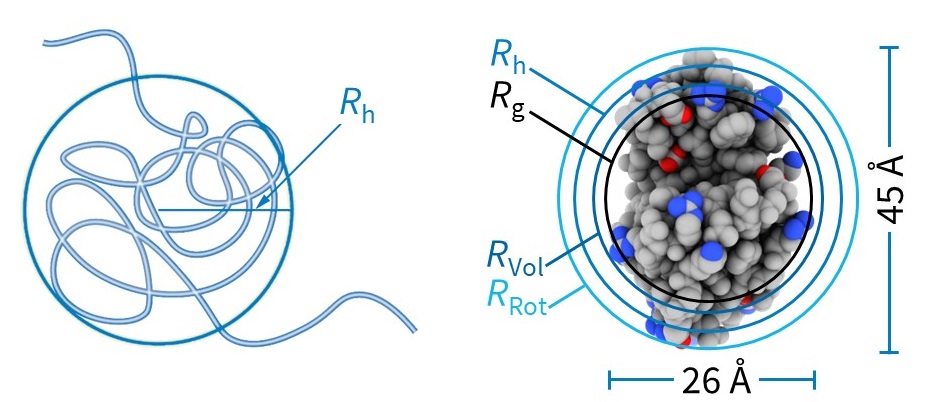
不同的尺寸测量技术，例如 DLS、小角度 X 射线散射、显微镜和分子建模可能会报告不同类型的半径。因此，重要的是要知道报告的“大小”是如何确定的，以及它是指分子的半径还是直径。 DLS 测量的 Rh 是与样品具有相同扩散系数的硬球的半径。其他度量包括 Rg（回转半径，或均方根半径，通过例如 MALS) 获得）、Rvol（与大分子占据相同体积的假设球体的半径）和 RRot（通过旋转大分子的半径）。图 3 说明了这些不同测量值如何比较紧凑的球状蛋白质溶菌酶。
分析粒度分布
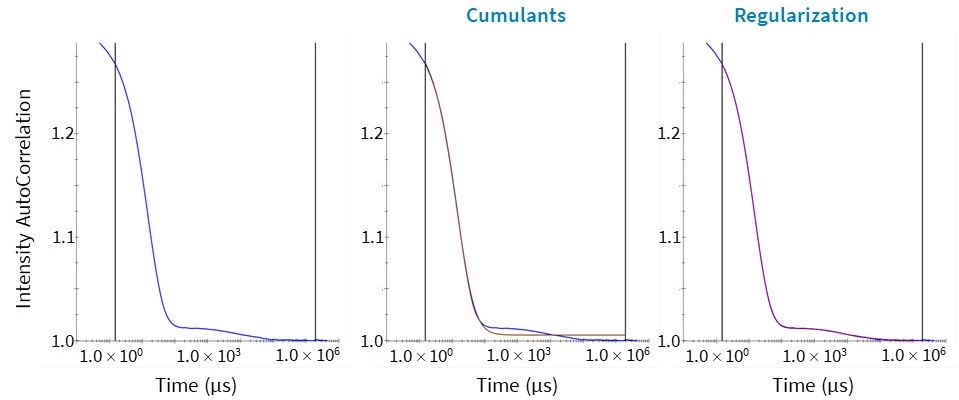
单机 DLS 无需色谱分离即可确定样品中的粒度分布和多个群体的存在，使其成为快速质量控制和大量样品高通量筛选的绝佳工具。具有 Rh 分布和相应扩散时间分布的样品的这种单机测量将产生由样品中所有粒子种类的自相关函数的总和描述的自相关函数，该自相关函数由它们的光散射强度加权。 Wyatt Technology 的 DYNAMICS®，DYNAMICS® Touch™ 和 ASTRA® 软件程序采用两种方法从此类复杂样品的单机测量中提取附加信息：累积量和正则化（图 4）。
Cumulants 方法假设一组粒子具有单一的平均扩散系数和关于该平均值的单一标准偏差。该算法可以拟合单分散或多分散的单峰样品（图 4），例如具有单体、二聚体和小寡聚体群体的纳米颗粒或蛋白质样品。
图 4. 显示了样本类型、适用于这些样本的拟合以及典型的正则化图。
相比之下，正则化方法假设存在任意数量的粒子群，每个粒子群都有自己的扩散系数、多分散性和标准偏差（即，Rh 的基本分布是平滑的）。正则化可以解决大小相差超过 3-5 倍的物种。这使其成为鉴定蛋白质样品中大聚集体和不溶性物质的首选方法。
对于每个峰或种类，正则化分析提供了广泛的指标，包括：
- 尺寸分布直方图（表 1 底部显示的示例）
- 平均半径
- % 多分散性
- 从测量半径估算的摩尔质量 （Mw-R）
- 每个群体散射的相对光强度 (% Intensity)、估算的相对质量量 (% Mass) 或粒子数 (% Number)
在 DYNAMICS 和 DYNAMICS Touch（图 5）中采集数据以及自动数据质量评估后，会立即显示累积量和正则化拟合及其相应的残差。这允许用户快速确定哪些测量符合数据质量标准，哪些需要仔细检查或重新审视，以及哪种方法最适合。
图 5.（左）多模态样本（蓝色）的自相关函数。 （中）累积量拟合自相关函数（棕色）。 （右）正则化拟合自相关函数（紫色）。对于这个多模态样本，Cumulants 拟合不能很好地拟合自相关函数。
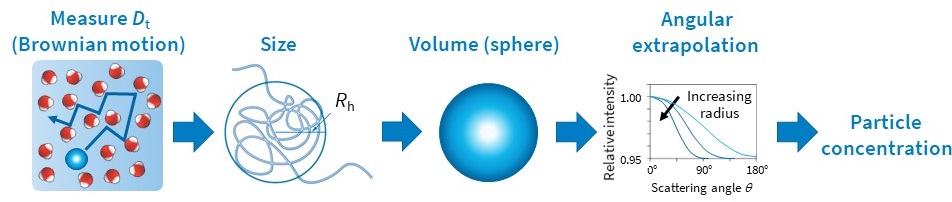
测量纳米粒子浓度
利用从扩散行为确定的流体动力学尺寸和总散射强度，可以测量另一个重要属性：纳米粒子的浓度，N。
计算需要粒子的体积 V 和折射率 nparticle，以及溶剂的折射率 n0 。还需要假设用户指定的形状模型（例如，均匀球体或涂层球体）。然后可以解释扩散系数以获得诸如半径的维度，由此计算粒子的体积（图6）。颗粒组成材料的折射率可以在文献中找到。每单位体积的粒子浓度 N 然后可以根据量化为零角过量瑞利比的光散射强度和以下方程确定（Van Holde, K. E. Physical biochemistry. Prentice-Hall, 1971）：
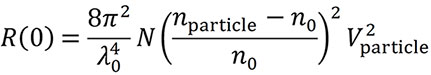
DynaPro Plate Reader 浓度测量的最大 Rh 为 160 nm，NanoStar 为 175 nm。更大尺寸和更复杂形状的颗粒需要多角度光散射 (MALS)，可以使用 Eclipse™ FFF-MALS 仪器进行探测。
图 6. DLS 可用于测量样品中的颗粒浓度。
表征分子间相互作用
非特异性分子间相互作用遍及自然界，并且具有多种物理起源，包括静电吸引和排斥、疏水和排除体积效应以及诱导偶极子。相互作用可以是吸引力或排斥力，并且在生物治疗剂的配方中很重要。
DynaPro NanoStar 和 DynaPro Plate Reader 都可以量化与 DLS 或 SLS 的大分子相互作用。 DLS 通过扩散相互作用参数 kD 评估非特异性相互作用和胶体稳定性。 SLS 量化第二维里系数 (A2)。 kD 和 A2 都代表特定溶剂中溶质-溶质相互作用的互补度量，对于理解相互作用和对公式进行排序都很有用。
在理想的稀释溶液中，由 DLS 测量的扩散系数 (Dt ) 不依赖于溶质浓度。随着浓度的增加，溶液变得不太理想，进行一阶展开；扩散相互作用参数 kD（单位为 mL/g）是对扩散系数的一阶修正，如下所示：
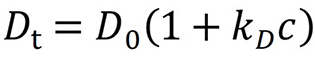
kD 是通过测量作为浓度函数的扩散系数来确定的，在应用一阶近似的浓度范围内（通常为 1 – 10 mg/mL）。
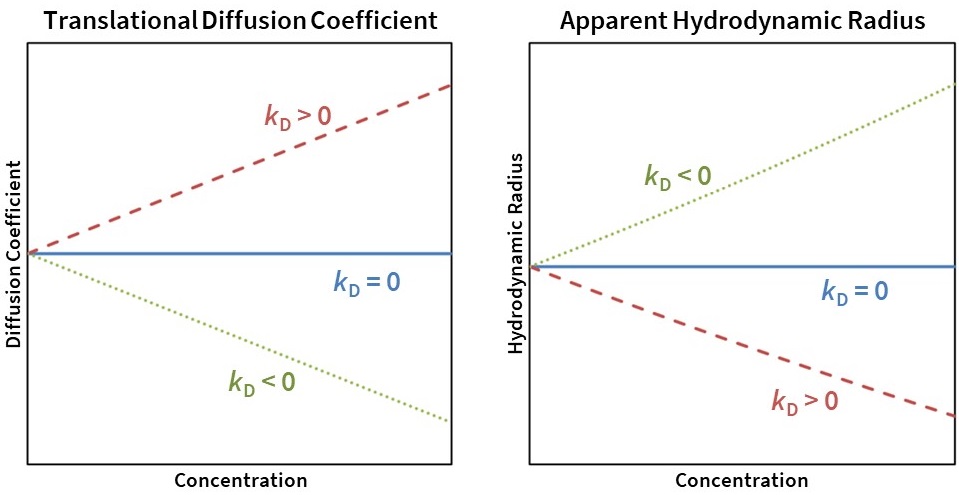
有吸引力的相互作用（kD < 0）导致 Dt 明显减少和 Rh 明显增加，而排斥相互作用（kD > 0）导致 Dt 明显增加和 Rh 明显减少（图 7） ）。 A2 接近排除体积值的硬球分子通常具有介于0和5 mL/g之间的 kD 值。
扩散相互作用参数不是一个纯粹的热力学量——它结合了热力学和流体力学的贡献。对于描述胶体相互作用的纯热力学量，通常探索第二维里系数。
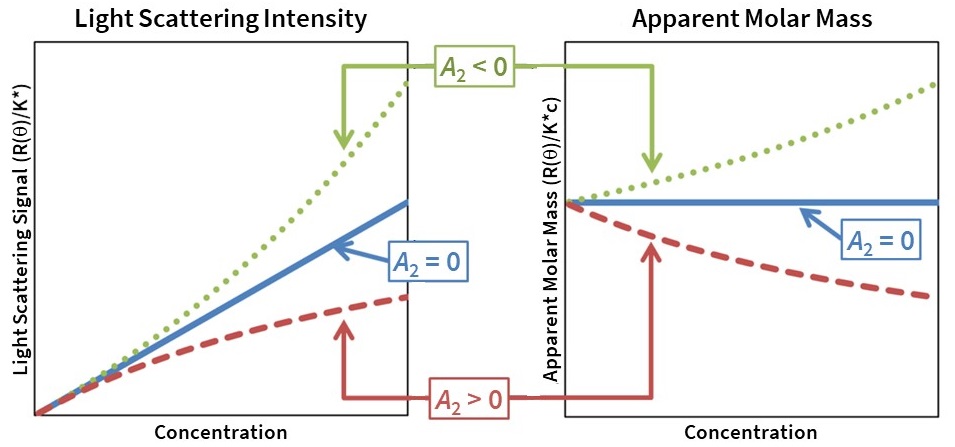
SLS 和 MALS 通过散射强度与浓度的测量获得的第二维里系数 A2 也报告了溶剂依赖性大分子自缔合和胶体稳定性。具体而言，有吸引力的相互作用（A2 < 0）导致散射强度比线性增加得更快并且产生摩尔质量的明显增加，并且排斥相互作用（A2 > 0）导致散射强度比线性增加得慢并且产生明显的摩尔质量减少（图8）。在色谱典型的低浓度下，A2 的影响可以忽略不计，并且 A2 可以设置为0用于数据分析。
图7. kD=0（实心蓝线），kD>0（红色虚线）和 kD<0（绿色虚线），平移扩散系数（左）和表观 Rh（右）作为浓度的函数。
图 8. 光散射强度（左）和表观摩尔质量（右）作为浓度函数的 A2 = 0（蓝色实线）、A2 > 0（红色虚线）和 A2 < 0（绿色虚线）线）。
了解自相关函数
在 DLS 中，随时间测量的光强度波动通过二阶相关函数 g(2) (τ) 进行量化。强度函数偏移延迟时间 (τ) 并计算自相关函数 g(τ)。定性地，自相关函数是衡量强度函数在随时间 τ 移动时与其自身的相似程度的度量。随着 τ 值的增加，函数达到基线 1。
更具体地说，如各种光散射文献（参见 Chu, B. Laser Light Scattering：Basic Principles and Practice；Academic Press：Boston，1991）所述，单分散样品的相关函数可以通过以下等式进行分析：
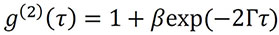
其中 β 是零延迟时的相关函数幅度，Γ 是衰减率，相关函数的基线在无限延迟时松弛到值 1。
DYNAMICS 和 ASTRA 使用非线性最小二乘拟合算法将测得的相关函数拟合到方程 2 中，以检索相关函数衰减率Γ。从这一点来看，Γ 可以通过以下关系转换为粒子的平移扩散系数 Dt：
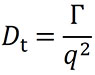
这里，q 是散射矢量的大小，由下式给出：
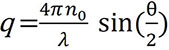
其中 n0 是溶剂的折射率，Λ0 是入射光的真空波长，q 是散射角。
最后，扩散系数可以通过斯托克斯-爱因斯坦方程解释为扩散球体的流体动力学半径 Rh：
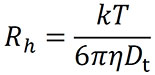
其中 k 是玻尔兹曼常数，T 是以 K 为单位的温度，h 是溶剂粘度（图 3）。