Die Grundlagen der Dynamischen Lichtstreuung
In Lösung befindliche Makromoleküle interagieren mit den Lösungsmittelmolekülen. Dies führt zu einer zufälligen Bewegung der Moleküle, die als Brown'sche Molekularbewegung bekannt ist. Betrachten Sie den Film von Partikeln mit 2 µm Durchmesser in reinem Wasser. Wie man sehen kann, ist jedes Teilchen ständig in Bewegung, und seine Bewegung ist unkorreliert mit den Bewegungen anderer Teilchen. (Film mit freundlicher Genehmigung von Dr. Eric R. Weeks, Emory University).
Brown'sche Molekularbewegung.
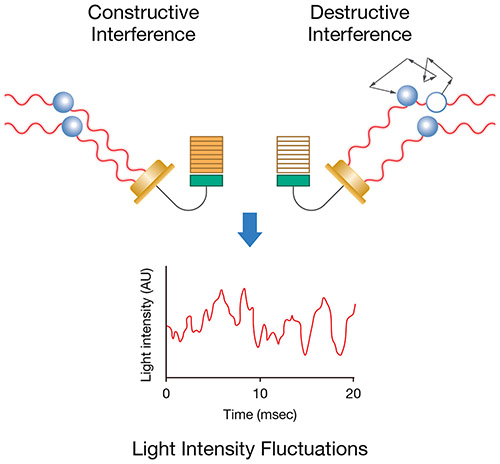
Da das Licht von den sich bewegenden Makromolekülen gestreut wird, verleiht diese Bewegung der Phase des gestreuten Lichts eine Zufälligkeit, so dass es bei der Addition des gestreuten Lichts von zwei oder mehr Teilchen zu einer wechselnden konstruktiven oder destruktiven Interferenz kommt. Dies führt zu zeitabhängigen Fluktuationen in der Intensität des gestreuten Lichts (Abb. 1).
Bei der dynamischen Lichtstreuung (DLS) werden die zeitabhängigen Fluktuationen im Streulicht durch ein Einzelphotonenzählmodul gemessen. Die Geschwindigkeit der Fluktuationen steht in direktem Zusammenhang mit der Diffusionsgeschwindigkeit des Moleküls durch das Lösungsmittel, die wiederum mit den hydrodynamischen Radien der Partikel zusammenhängt. Kleinere Teilchen diffundieren schneller und verursachen schnellere Schwankungen der Intensität als größere Teilchen. Daher enthält die Fluktuation der Lichtintensität Informationen über die Diffusion der Moleküle und kann verwendet werden, um einen Diffusionskoeffizienten zu extrahieren und eine Partikelgröße zu berechnen.
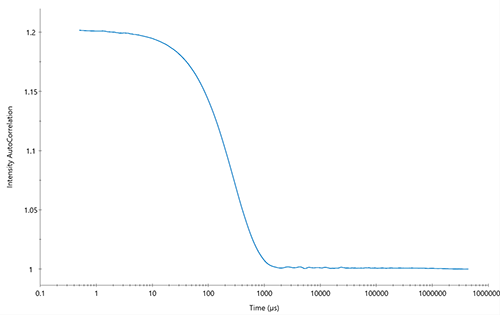
DLS wird vom DynaPro™ NanoStar™, dem DynaPro™ Plate Reader, dem ZetaStar™ und dem WyattQELS™-Module für MALS-Detektoren zur Bestimmung der effektiven Partikelgröße eingesetzt. Der translatorische Diffusionskoeffizient des Analyten Dt wird durch den Fit der Autokorrelationsfunktion bestimmt. Dadurch wird die gemessenen zeitabhängigen Fluktuationen der Lichtstreuintensität quantitativ beschrieben. Die Analyse erfolgt direkt in der zugehörigen Software DYNAMICS™ , DYNAMICS Touch™ oder ASTRA™ . Eine typische Autokorrelationsfunktion für eine monodisperse Probe ist in Abb. 2 dargestellt.
Die Stokes-Einstein-Gleichung liefert dann den hydrodynamischen Radius Rh, (Abb. 3) der dem gemessenen Dt entspricht:
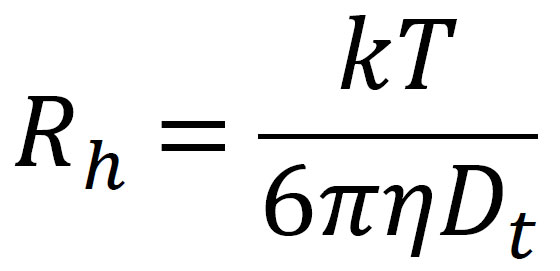
wobei k die Boltzmann-Konstante, T die Temperatur in Kelvin und h die Viskosität des Lösungsmittels ist.
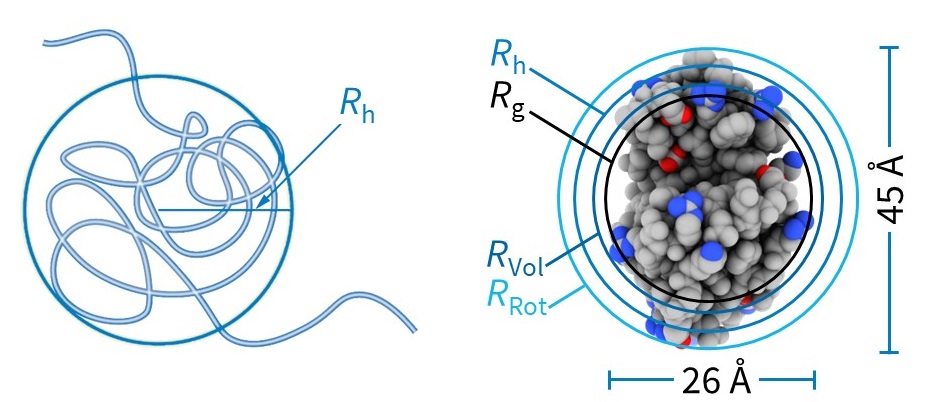
Verschiedene Größenbestimmungstechniken, z. B. DLS, Röntgenkleinwinkelstreuung, Mikroskopie und Molekülmodellierung, können unterschiedliche Arten von Radien angeben. Es ist daher wichtig zu wissen, wie eine angegebene "Größe" bestimmt wurde und ob sie sich auf den Radius oder den Durchmesser des Moleküls bezieht. Der durch DLS gemessene Rh ist der Radius einer harten Kugel mit dem gleichen Diffusionskoeffizienten wie die Probe. Andere Maße sind Rg (der Gyrationsradius oder der quadratische Wurzelradius, der z. B. mit MALS ermittelt wird), Rvol (der Radius einer hypothetischen Kugel, die das gleiche Volumen wie das Makromolekül einnimmt) und RRot (der Radius, der durch die Drehung des Makromoleküls entsteht). Abb. 3 veranschaulicht den Vergleich dieser verschiedenen Maße für das kompakte, kugelförmige Protein Lysozym.
Abbildung 1: Die Brown‘sche Bewegung führt zu messbaren Schwankungen der Lichtintensität im Laufe der Zeit.
Abbildung 2: Autokorrelationsfunktion für eine monodisperse Probe mit einem Partikelradius von 50 nm.
Abbildung 3 (links) Rh ist der Radius einer harten Kugel mit dem gleichen Diffusionskoeffizienten wie die Probe. (Rechts) Kompakte Moleküle, z. B. globuläre Proteine wie Lysozym, haben im Allgemeinen Rg < Rh.
Analyse von Partikelgrößenverteilungen
Batch-DLS kann Größenverteilungen und das Vorhandensein mehrerer Populationen in einer Probe bestimmen, ohne dass eine chromatografische Trennung erforderlich ist, was es zu einem ausgezeichneten Instrument für die schnelle Qualitätskontrolle und das Screening einer großen Anzahl von Proben im Hochdurchsatz macht. Solche Chargenmessungen von Proben mit einer Rh-Verteilung und einer entsprechenden Verteilung der Diffusionszeiten ergeben Autokorrelationsfunktionen, die durch die Summe der Autokorrelationsfunktionen aller Partikelspezies in der Probe, gewichtet mit ihren Lichtstreuintensitäten, beschrieben werden. Die Softwareprogramme DYNAMICS, DYNAMICS Touch und ASTRA von Wyatt Technology™ enthalten zwei Methoden zur Gewinnung zusätzlicher Informationen aus Chargenmessungen solch komplexer Proben: Kumulantenanalyse und Regularisierungsanalyse (Abb. 4).
Die Kumulantenmethode geht von einer Partikelpopulation mit einem einzigen durchschnittlichen Diffusionskoeffizienten und einer einzigen Standardabweichung um diesen Durchschnitt aus. Der Algorithmus eignet sich für monomodale Proben, die monodispers oder polydispers sind (Abb. 4), wie etwa Nanopartikel oder Proteinproben mit Populationen von Monomeren, Dimeren und kleinen Oligomeren.
Bei der Regularisierungsmethode hingegen wird von einer beliebigen Anzahl von Partikelpopulationen ausgegangen, von denen jede ihren eigenen Diffusionskoeffizienten, ihre eigene Polydispersität und ihre eigene Standardabweichung hat. Die Regularisierung kann Spezies auflösen, die sich in ihrer Größe um mehr als das 3-5fache unterscheiden. Dies macht sie zur Methode der Wahl für die Identifizierung großer Aggregate und unlöslicher Spezies in Proteinproben.
Für jeden Peak oder jede Spezies liefert die Regularisierungsanalyse eine breite Palette von Parametern, darunter:
- ein Histogramm der Größenverteilung (Beispiele in der unteren Zeile von Tabelle 1)
- mittlerer Radius
- % Polydispersität
- die aus dem gemessenen Radius geschätzte molare Masse (Mw-R)
- die relative Lichtintensität, die von jeder Population gestreut wird (%Intensität), die geschätzte relative Menge an Masse (%Masse) oder die Anzahl der Partikel (%Anzahl).
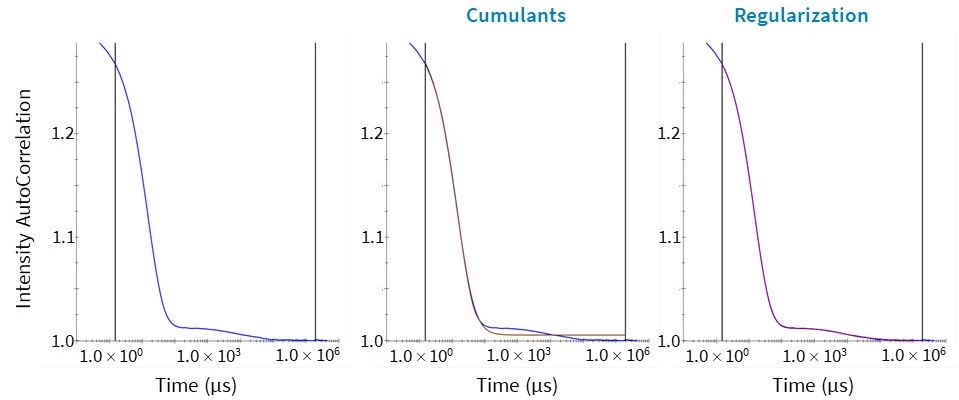
Kumulanten- und Regularisierungsfits und ihre entsprechenden Abweichungen werden sofort nach der Datenerfassung in DYNAMICS und DYNAMICS Touch (Abb. 5) angezeigt, zusammen mit einer automatischen Bewertung der Datenqualität. So kann der Benutzer schnell feststellen, welche Messungen den Datenqualitätsstandards entsprechen, welche überprüft oder überarbeitet werden müssen und welche Methode die beste Anpassung liefert.
Abbildung 5: (Links) Autokorrelationsfunktion einer multimodalen Stichprobe (blau). (Mitte) Die Kumulantenanpassung an die Autokorrelationsfunktion (braun). (Rechts) Die Regularisierungsanpassung an die Autokorrelationsfunktion (violett). Die Kumulantenanpassung passt die Autokorrelationsfunktion für diese multimodale Stichprobe nicht gut an.
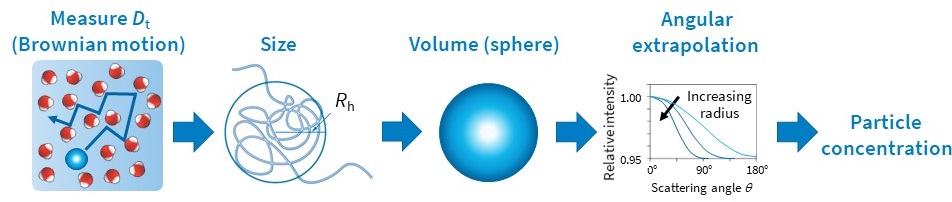
Messung von Nanopartikelkonzentration
Unter Nutzung der Bestimmung der hydrodynamischen Größe aus dem Diffusionsverhalten und der gesamten Streuintensität kann eine weitere wichtige Eigenschaft gemessen werden: die Anzahl der Nanopartikel pro Volumeneinheit, N.
Für die Berechnung werden das Volumen V und der Brechungsindex nPartikel, der Partikel sowie der Brechungsindex n0 des Lösungsmittels benötigt. Die Annahme eines benutzerspezifischen Formmodells z. B. einheitliche Kugel oder beschichtete Kugel ist ebenfalls erforderlich. Dann kann der Diffusionskoeffizient interpretiert werden, um eine Dimension wie den Radius zu erhalten, aus dem das Volumen des Partikels berechnet wird (Abb. 6). Der Brechungsindex des Materials, aus dem die Partikel bestehen, kann in der Literatur nachgelesen werden. Die Partikelkonzentration pro Volumeneinheit, N, kann dann aus der Lichtstreuintensität, die als Überschuss-Rayleigh-Verhältnis bei Winkel Null quantifiziert wird und der folgenden Gleichung bestimmt werden (Van Holde, K. E. Physical biochemistry. Prentice-Hall, 1971):
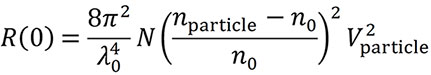
Das maximale Rh für Konzentrationsmessungen beträgt 160 nm für den DynaPro Plate Reader und 175 nm für den DynaPro NanoStar. Partikel, die größer sind und komplexere Formen haben, erfordern eine Mehrwinkel-Lichtstreuung (MALS) und können mit dem Eclipse™ FFF-MALS-System untersucht werden.
Charakterisierung intermolekularer Wechselwirkungen
Unspezifische intermolekulare Wechselwirkungen sind in der Natur überall anzutreffen und haben vielfältige physikalische Ursachen wie elektrostatische Anziehung und Abstoßung, hydrophobe und ausgeschlossene Volumeneffekte sowie induzierte Dipole. Die Wechselwirkungen können anziehend oder abstoßend sein und sind für die Formulierung von Biotherapeutika von Interesse.
Sowohl der DynaPro NanoStar als auch der DynaPro Plate Reader können makromolekulare Wechselwirkungen mit DLS und/oder SLS quantifizieren. DLS bewertet unspezifische Wechselwirkungen und kolloidale Stabilität über den Diffusionswechselwirkungsparameter kD. SLS quantifiziert den zweiten Virialkoeffizienten (A2). Sowohl kD als auch A2 stellen komplementäre Messgrößen für die Wechselwirkung zwischen gelöster Substanz und Lösungsmittel in einem bestimmten Lösungsmittel dar und sind sowohl für das Verständnis von Wechselwirkungen als auch für die Einstufung von Formulierungen nützlich.
In einer ideal verdünnten Lösung ist der mit DLS gemessene Diffusionskoeffizient (Dt) nicht von der Konzentration des gelösten Stoffes abhängig. Mit zunehmender Konzentration wird die Lösung weniger ideal, und es wird eine Expansion erster Ordnung durchgeführt. Für den Diffusionsinteraktionsparameter kD (in Einheiten von mL/g) ist die Korrektur erster Ordnung des Diffusionskoeffizienten wie folgt:
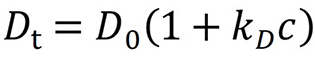
kD wird durch Messung des Diffusionskoeffizienten als Funktion der Konzentration in dem Konzentrationsbereich bestimmt, in dem die Näherung erster Ordnung gilt (typischerweise 1 - 10 mg/mL).
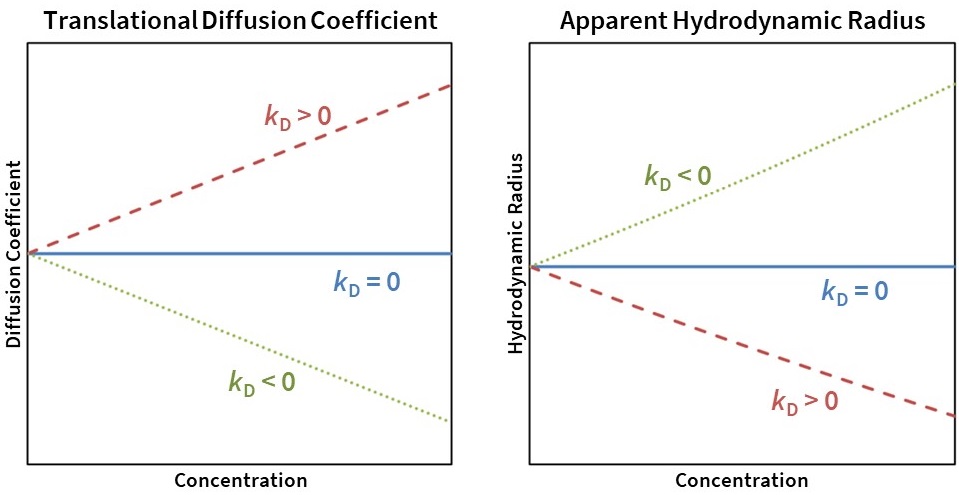
Anziehende Wechselwirkungen (kD < 0) führen zu einer scheinbaren Abnahme von Dt und einer scheinbaren Zunahme von Rh, während abstoßende Wechselwirkungen (kD > 0) zu einer scheinbaren Zunahme von Dt und einer scheinbaren Abnahme von Rh führen (Abb. 7). Moleküle, die sich wie harte Kugeln verhalten und bei denen A2 nahe am Wert des ausgeschlossenen Volumens liegt, haben typischerweise kD-Werte zwischen 0 und 5 mL/g.
Der Diffusionswechselwirkungsparameter ist keine rein thermodynamische Größe, sondern kombiniert thermodynamische und hydrodynamische Beiträge. Für eine rein thermodynamische Größe, die kolloidale Wechselwirkungen beschreibt, wird üblicherweise der zweite Virialkoeffizient verwendet.
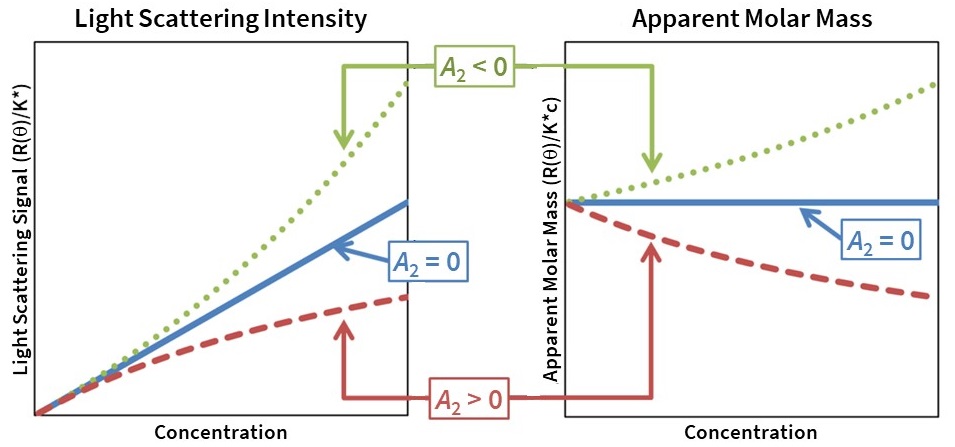
Der zweite Virialkoeffizient A2, der mit SLS und MALS durch Messungen der Streuintensität in Abhängigkeit von der Konzentration ermittelt wird, gibt auch Auskunft über die lösungsmittelabhängige makromolekulare Selbstassoziation und kolloidale Stabilität. Insbesondere führen anziehende Wechselwirkungen (A2 < 0) dazu, dass die Streuintensität überproportional ansteigt und zu einer scheinbaren Zunahme der molaren Masse führt, während abstoßende Wechselwirkungen (A2 > 0) dazu führen, dass die Streuintensität unterproportional ansteigt und zu einer scheinbaren Abnahme der molaren Masse führt (Abb. 8). Bei niedrigen Konzentrationen, wie sie für die Chromatographie typisch sind, ist die Wirkung des A2 vernachlässigbar, und er kann für die Datenanalyse auf 0 gesetzt werden.
Abbildung 7: Translationsdiffusionskoeffizient (links) und scheinbares Rh (rechts) als Funktion der Konzentration für kD = 0 (durchgezogene blaue Linie), kD> 0 (gestrichelte rote Linie) und kD < 0 (gepunktete grüne Linie).
Die Autocorrelation Funktion verstehen
In der DLS Analyse werden die zeitlichen Schwankungen der Streulichtintensität über eine Korrelationsfunktion zweiter Ordnung g(2) (τ) quantifiziert. Die Funktion der Intensität wird um eine Verzögerungszeit (τ) verschoben und die Autokorrelationsfunktion g(τ) berechnet. Qualitativ gesehen ist die Autokorrelationsfunktion ein Maß dafür, wie ähnlich die Intensitätsfunktion sich selbst ist, wenn sie um die Zeit τ verschoben wird. Wenn der Wert von τ zunimmt, erreicht die Funktion eine Basislinie von 1.
Genauer gesagt, und wie in verschiedenen Texten über Lichtstreuung beschrieben (vgl. Chu, B. Laser Light Scattering: Basic Principles and Practice; Academic Press: Boston, 1991), kann die Korrelationsfunktion für eine monodisperse Probe durch die folgende Gleichung analysiert werden:
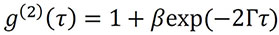
wobei β die Amplitude der Korrelationsfunktion bei einer Verzögerung von Null ist, Γ die Abklingrate ist und die Basislinie der Korrelationsfunktion bei unendlicher Verzögerung auf den Wert 1 zurückgeht.
DYNAMICS und ASTRA verwenden einen nichtlinearen Algorithmus zur Anpassung der gemessenen Korrelationsfunktion an Gleichung 2, um die Abklingrate der Korrelationsfunktion Γ zu ermitteln. Von diesem Punkt aus kann Γ über die folgende Beziehung in den Translationsdiffusionskoeffizienten Dt für das Teilchen umgewandelt werden:
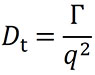
Hier ist q die Größe des Streuvektors und wird beschrieben durch:
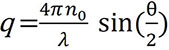
wobei n0 der Brechungsindex des Lösungsmittels, Λ die Vakuumwellenlänge des einfallenden Lichts und q der Streuwinkel ist.
Schließlich kann der Diffusionskoeffizient über die Stokes-Einstein-Gleichung als der hydrodynamische Radius Rh einer diffundierenden Kugel interpretiert werden:
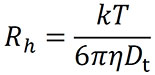
wobei k die Boltzmann-Konstante, T die Temperatur in K und h die Viskosität des Lösungsmittels ist (Abb. 3).