Grundlagen der Elektrophoretischen Lichtstreuung
Die elektrophoretische Lichtstreuung (ELS) ist eine optische Technik zur Messung der elektrophoretischen Mobilität von Partikeln in Lösung oder Suspension. In Kombination mit der Kenntnis des hydrodynamischen Radius der Partikel und anderer Parameter ermöglicht die ELS die Bestimmung des Zetapotenzials und der effektiven Ladung.
Theorie
ELS: Elektrophoretische Mobilität
Elektrophorese ist die Wanderung von Makromolekülen und dispergierten Teilchen unter dem Einfluss eines elektrischen Feldes. Die elektrophoretische Mobilität µE ist definiert als:
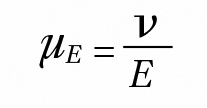 (1)
(1)
wobei v die elektrophoretische Geschwindigkeit der Partikel und E das angelegte elektrische Feld ist.
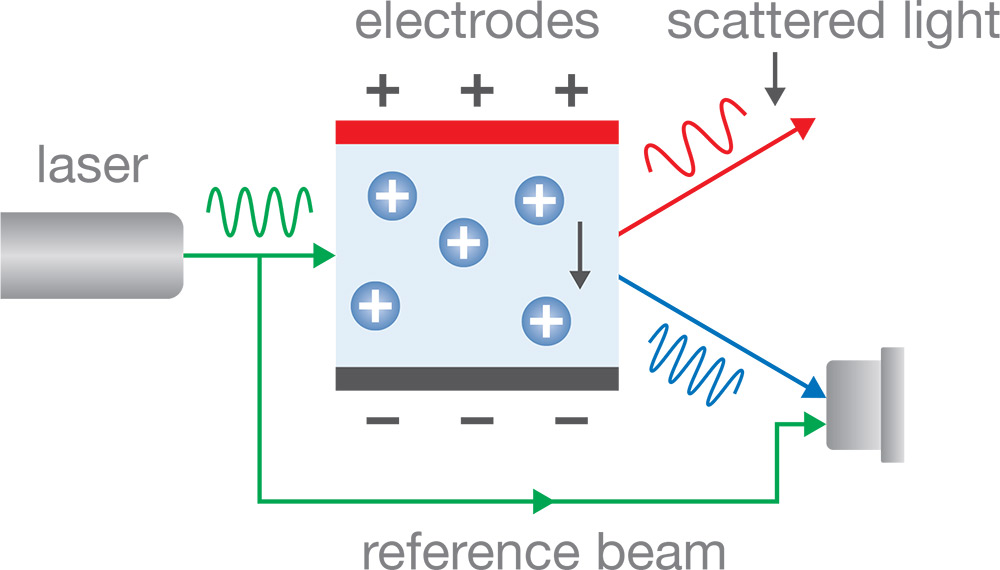
Bei ELS wird eine Probenzelle, die optische Fenster und Elektroden enthält, mit einem hochkohärenten Laserstrahl beleuchtet. Beim Anlegen einer Spannung an die Elektroden wandern die Partikel und erreichen eine bestimmte Geschwindigkeit, deren Größe und Richtung von der Größe und Oberflächenladung der Partikel sowie der Viskosität und Leitfähigkeit der Lösung abhängen. Diese Geschwindigkeit führt zu einer Doppler-Verschiebung des von den Teilchen gestreuten Lichts, wie rechts dargestellt. Das gestreute Licht ist rot- oder blauverschoben (d. h. die optische Frequenz nimmt ab bzw. zu), je nachdem, in welche Richtung die Partikel relativ zum Streuwinkel wandern.
Die Dopplerfrequenzverschiebung Δf des gestreuten Lichts, die mit v in Beziehung steht, ist
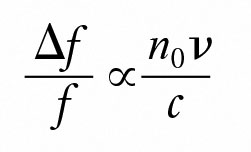 (2)
(2)
wobei:
c die Geschwindigkeit des Lichts im Vakuum ist.
n0 ist der Brechungsindex des Lösungsmittels.
f ist die Frequenz des einfallenden Lichts.
Obwohl die Dopplerverschiebung Δf der Teilchen, die mit ELS gemessen werden kann, im Vergleich zur Lichtfrequenz winzig ist (Δf/f < 0.000000000001!), kann sie mit Hilfe der Interferometrie bestimmt werden. Ein abgespaltener Teil des einfallenden Strahls, der so genannte Referenzstrahl, wird um die Probenzelle herumgeleitet und mit dem einfallenden Licht, das in Richtung Detektor gestreut wurde, kombiniert. Die Interferenz zwischen den beiden Strahlen erzeugt auf dem Detektor periodische Intensitätsschwankungen mit einer Frequenz von Δf/f.
ELS + DLS: Zetapotenzial und effektive Ladung
Dank des unabhängigen dynamischen Lichtstreumoduls im ZetaStar™ kann der hydrodynamische Radius Rhdes Partikels gleichzeitig mit der Mobilität gemessen werden, um das Zetapotenzial ζ und die Molekülladung zu berechnen. Das Zetapotenzial ist das elektrische Potenzial um das Teilchen auf der Gleitebene, d. h. der Radius, innerhalb dessen sich die vom Teilchen angezogenen Gegenionen mit dem Teilchen bewegen, während sich die Ionen außerhalb dieses Radius unabhängig vom Teilchen bewegen.
In dem Grenzfall, in dem der hydrodynamische Radius viel größer ist als die Dicke der ionischen Doppelschicht, wird die Smoluchowski-Gleichung gemäß Gleichung 3 verwendet:
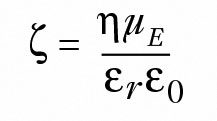 (3)
(3)
wobei η die Viskosität der Lösung, εr die Dielektrizitätskonstante des Lösungsmittels und ε0 die Permittivität des Vakuums ist.
Wenn Rh viel kleiner als die Doppelschichtdicke ist, wird stattdessen die Hückelsche Gleichung nach Gleichung 4 verwendet:
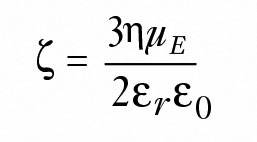 (4)
(4)
Der ZetaStar kann auch die molekulare Debye-Hückel-Henry-Ladung ZDHHe es Teilchens über die Beziehung in Gleichung 5 bestimmen
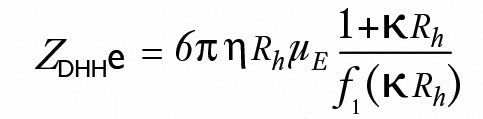 (5)
(5)
Dabei ist κ die inverse Debye-Länge (berechnet aus der Leitfähigkeit σ, die von ZetaStar gemessen wird) und f1(κ Rh) ie Henry-Funktion*.
Referenzen
* Tanford, C. Physical Chemistry of Macromolecules; Wiley: New York, 1961.
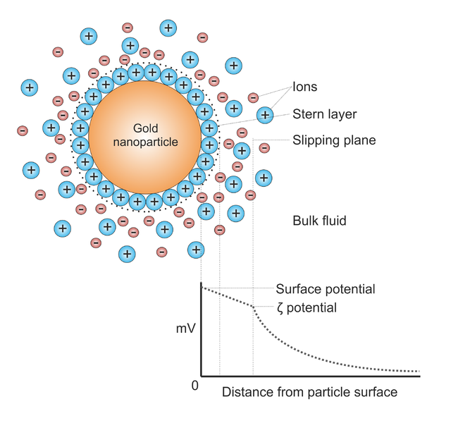
Diagramm, das die Ionenkonzentration und die Potenzialdifferenz als Funktion des Abstands von der geladenen Oberfläche eines in einem Dispersionsmedium suspendierten Teilchens zeigt. Larryisgood, CC BY-SA 3.0 https://creativecommons.org/licenses/by-sa/3.0, via Wikimedia Commons.
Technologie
Konventionelles PALS
Die Intensitätsschwankungen am Detektor, die durch die Interferenz zwischen dem Referenzstrahl und dem gestreuten Licht erzeugt werden, reichen aus, um die Größe von Δf zu bestimmen, nicht aber sein Vorzeichen, das das Vorzeichen des Zetapotenzials oder der Ladung vermittelt. Um das Vorzeichen von Δf zu bestimmen, wird bei der konventionellen ELS eine Technik namens phasenanalytische Lichtstreuung (PALS) eingesetzt, bei der ein Paar oszillierender Spiegel dem Referenzstrahl eine zusätzliche Frequenzverschiebung verleiht. Die Verfolgung der relativen Phase zwischen der mechanischen Bewegung der Spiegel und der des Detektorsignals liefert die zusätzlichen Informationen, die zur Bestimmung des Vorzeichens von Δf erforderlich sind. Die zusätzliche Frequenz liegt jedoch im Bereich des typischen mechanischen Rauschens, und das optische System selbst muss genau eingestellt werden, um die Ausrichtung der Strahlen aufrechtzuerhalten. Diese beiden Probleme machen herkömmliche PALS relativ unzuverlässig und erfordern möglicherweise eine regelmäßige Wartung.
FIDELIS™
Um die Unzulänglichkeiten herkömmlicher PALS zu überwinden, entwickelte Wyatt eine neue Technologie, die faserinterferometrische elektrophoretische Doppler-Lichtstreuung (FIDELIS), die im DynaPro™ ZetaStar™ eingesetzt wird. Bei FIDELIS wird das bewegliche Spiegelpaar durch ein gekoppeltes Paar akusto-optischer Modulatoren ersetzt, d. h. Geräte, die die Weglänge bei viel höheren Frequenzen modulieren, als dies bei der mechanischen Bewegung von Spiegeln möglich ist. Dieses System ermöglicht eine Modulation mit kHz-Frequenzen, so dass die Schwebungsfrequenz am Detektor nun fAOM+ Δf beträgt, wobeifAOM die Modulationsfrequenz ist, die von den akusto-optischen Modulatoren erzeugt wird. Das Vorzeichen von Δf wird als Differenz der Schwebungsfrequenz relativ zu fAOM erkannt..
Darüber hinaus ist das gesamte optische System von FIDELIS fasergekoppelt, so dass der gesamte optische Referenzpfad monolithisch ist und keine Optik im freien Raum vorhanden ist, ebenso wie die Kopplung der einfallenden und gestreuten Strahlen zur und von der Probenzelle.
FIDELIS und ZetaStar erfüllen die Anforderungen moderner ELS-Instrumente in zweierlei Hinsicht:
- Die Hochfrequenz-Phasenmodulation verschiebt die interferometrischen Schwebungen von ~ 100 Hz auf ~ 10000 Hz, einen Bereich, der weit außerhalb des mechanischen Rauschens liegt und einen hohen Signal-Rausch-Abstand und eine hohe Empfindlichkeit sowie eine inhärente Erkennung des Vorzeichens von Δf ermöglicht.
- Die fasergekoppelte Optik sorgt für die mühelose Beibehaltung des größten Teils der optischen Ausrichtung und der optischen Oberflächenreinheit. Die FIDELIS-Technologie besteht aus einer Reihe von vor Ort austauschbaren Modulen, die eine maximale Betriebszeit des Geräts und die Produktivität des Benutzers gewährleisten.
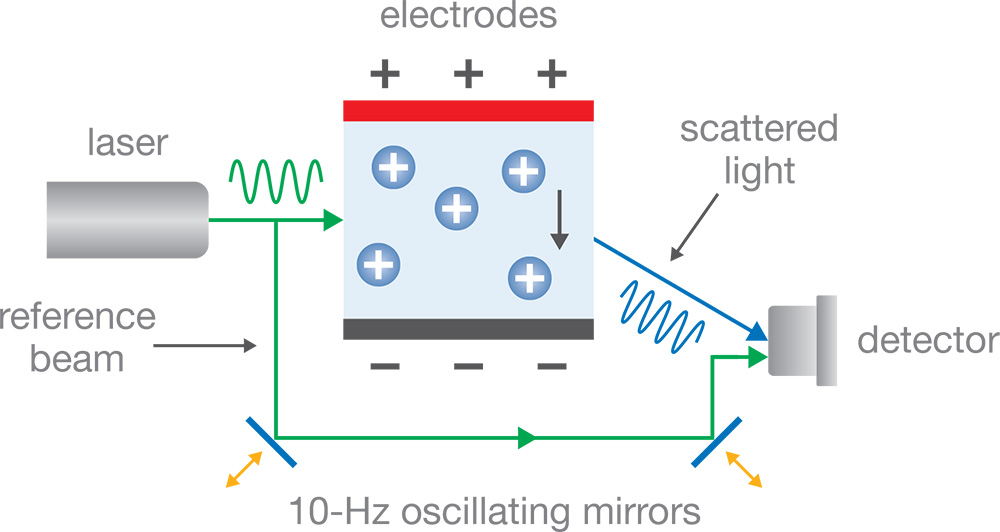
Abbildung 1: Bei der herkömmlichen elektrophoretischen Lichtstreuung zur Phasenanalyse werden die Spiegel mechanisch bewegt, um die optische Weglänge zu modulieren. Leichte Fehlausrichtungen des Lasers, der Spiegel und des Detektors können die Zuverlässigkeit der Daten beeinträchtigen.

Abbildung 2: Die FIDELIS-Technologie, die im DynaPro ZetaStar zum Einsatz kommt, verwendet fasergekoppelte Elemente: Laser, Splitter, akustooptischer Modulator und Strahlkombinierer für ein robustes und monolithisches optisches ELS-System mit hervorragender Empfindlichkeit und Geschwindigkeit.
{“labels”:[],”rewrite”:{“with_front”:true}}
