了解 Electrophoretic Light Scattering
电泳光散射(Electrophoretic light scattering、ELS)是一种光学技术,用于测量溶液或悬浮液中颗粒的电泳迁移率。 结合对颗粒的流体动力学半径和其他参数的了解,ELS能够确定ζ电位和有效电荷。
基础理论
ELS:电泳迁移率
电泳是大分子和分散颗粒在电场影响下的迁移过程。电泳迁移率µE具体公式为:
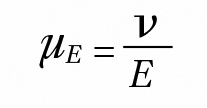 (1)
(1)
v指的是粒子电泳速度,E指的是施加的电场。
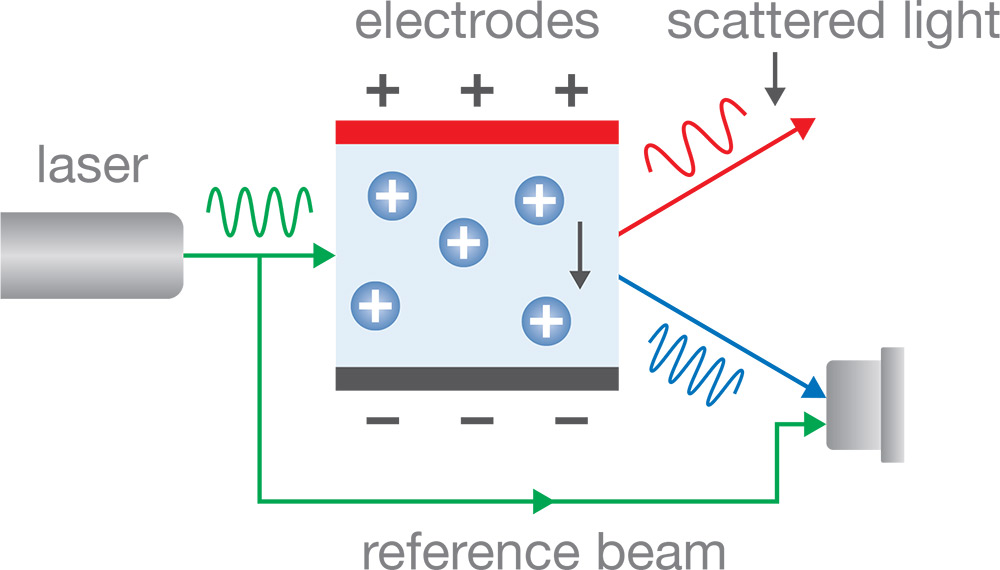
ELS使用一个包含光学窗口和电极的流通池,被强相干光照射。在电极施加电压时,颗粒迁移并达到一定速度,其大小和方向取决于颗粒的大小、表面电荷以及溶液的粘度和电导率。 该速度导致颗粒散射的光发生多普勒频移,如右图所示。散射的光可以发生red-shifted或blue-shifted,具体取决于颗粒相对于散射角度的迁移方向。如果颗粒迁移方向与散射角度相反,光将发生red-shifted,即光的光学频率减小。如果颗粒迁移方向与散射角度相同,光将发生blue-shifted,即光的光学频率增加。
多普勒频移Δf与颗粒速度v之间存在关系:
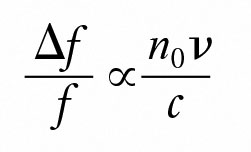 (2)
(2)
这里:
c是真空中的光速。
n0是溶剂的折射率。
f是入射光的频率。
尽管颗粒引起的 ELS 可测量的多普勒频移Δf相对于光频率来说非常微小(Δf/f < 0.000000000001!),但可以通过干涉测量来确定。 干涉测量的技术是通过将光束分成两部分来测量多普勒频移。第一部分被称为“参考光束”,另一部分是照射到样品并散射的部分。参考光束沿着流通池的周围路径,不与样品发生相互作用。参考光束最终与从样品散射而来的光束相结合。两个光束在检测器上相遇,产生干涉。这种干涉导致检测器上出现周期性的强度波动,频率为Δf/f。
ELS + DLS:ζ电位和有效电荷
在 ZetaStar™ 中,由于独立的动态光散射模块,可以同时测量颗粒的流体动力学半径(Rh)和迁移率,以计算 zeta 电位(ζ)和分子电荷。Zeta 电位表示颗粒在光滑平面周围的电势,即在该半径内,被吸引到颗粒的对离子随颗粒移动,而在该半径外,离子独立于颗粒移动。
在流体动力学半径远大于离子双层厚度的极端情况下,使用 Smoluchowski 的方程,如图所示:
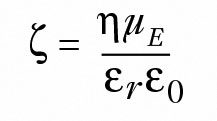 (3)
(3)
其中 η 是溶液粘度,εr是溶剂介电常数,而ε0是真空介电常数。
或者,在Rh远小于双层厚度的情况下,使用 Hückel 的方程,如图所示:
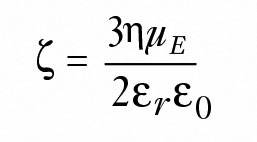 (4)
(4)
ZetaStar 还可以通过如下方程中的关系确定颗粒的分子 Debye-Hückel-Henry charge ZDHHe:
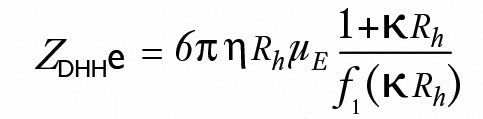 (5)
(5)
在这个关系中,κ 是逆 Debye 长度(从 ZetaStar 测得的电导率 σ 计算得到),而 f1(κ Rh) 是 Henry's 函数*。
参考文献
* Tanford, C. Physical Chemistry of Macromolecules; Wiley: New York, 1961.
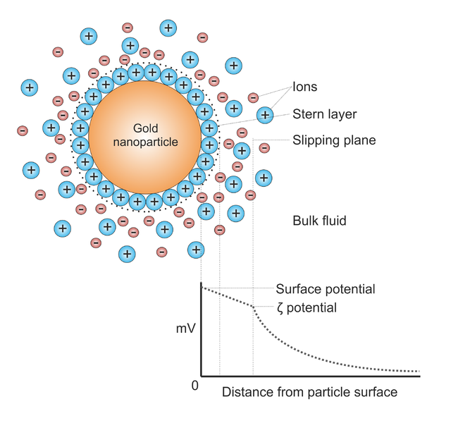
示意图展示了悬浮在分散介质中的颗粒带电表面附近的离子浓度和电势差随距离变化的关系。Larryisgood, CC BY-SA 3.0 https://creativecommons.org/licenses/by-sa/3.0, via Wikimedia Commons.
基础技术
传统 PALS(相位分析光散射)
参考光束和散射光之间的干涉在探测器上产生的振荡强度足以确定Δf的大小,但它难以准确确定这种变化的符号,即无法确定 zeta 电位的符号。为了解决这个问题,传统 ELS 使用了相位分析光散射技术,在这种技术中,一对振动镜使参考光发生额外的频率变化。通过跟踪振动镜的机械运动与检测信号的相对相位,可以提供确定 Δf 的符号所需的额外信息。然而,这个额外的频率通常在典型的机械噪声范围内,并且光学系统本身需要精湛的调整以保持光束的对准。这两个问题使传统 PALS 相对不可靠,并可能需要定期维护。
纤维干涉多普勒电泳光散射(FIDELIS)
为了克服传统 PALS 的不足,Wyatt 开发了一种新技术,即 FIDELIS™,应用于 DynaPro™ ZetaStar。在 FIDELIS 中,一对振动镜被一对耦合的声光调制器取代,这些设备以比振动镜的机械运动更高的频率调制光程。事实上,这个系统提供 kHz 频率调制,因此检测器处的拍频现在是fAOM+ Δf,其中fAOM是声光调制器赋予的调制频率。基于拍频相对于fAOM的差异,Δf的符号可以被检测到。
此外,整个 FIDELIS 光学系统是纤维耦合的,使整个参考光路成为整体,可自由更换整个模组,入射光和散射光与样品池之间的耦合也同样可以整个更换。
FIDELIS和ZetaStar在两个方面满足现代ELS仪器的需求:
- 高频相位调制将干涉拍频从约100赫兹提高到约10000赫兹,远远超出了机械噪声的范围,从而实现了高信噪比和灵敏度,以及对Δf符号的固有检测。
- 纤维耦合光学轻松维持了光学对准和光学表面的清洁度。FIDELIS技术由一组可更换的模块组成,以实现最大程度的仪器正常运行时间和用户生产力。
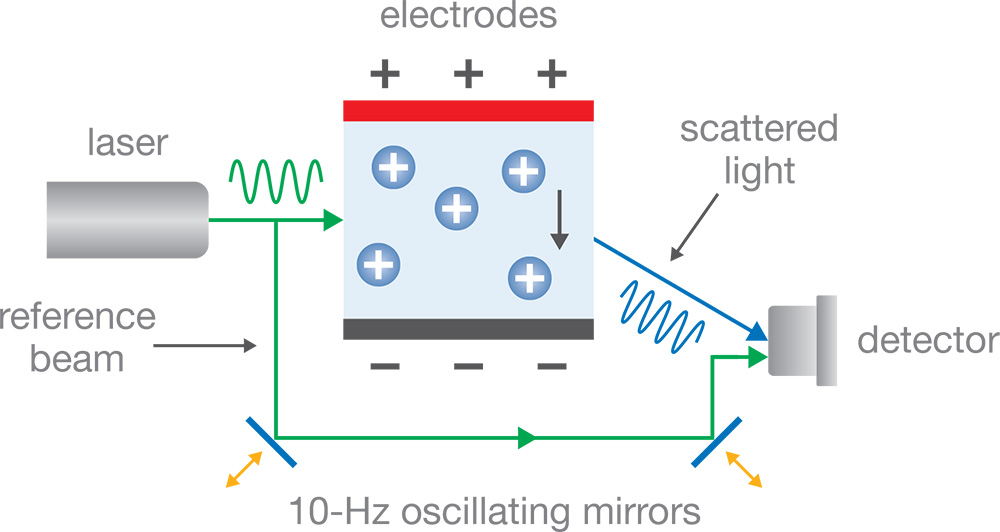
图1显示了传统相位分析电泳光散射,使用机械振动的镜子来调制光学路径长度。激光、镜子和检测器的轻微错位可能影响数据的可靠性。

图2展示了应用于 DynaPro ZetaStar 的 FIDELIS 技术,采用纤维耦合元件:激光、分光器、声光调制器和光束合并器,构建了稳健的 ELS 光学系统,提供出色的灵敏度和速度。
{“labels”:[],”rewrite”:{“with_front”:true}}
