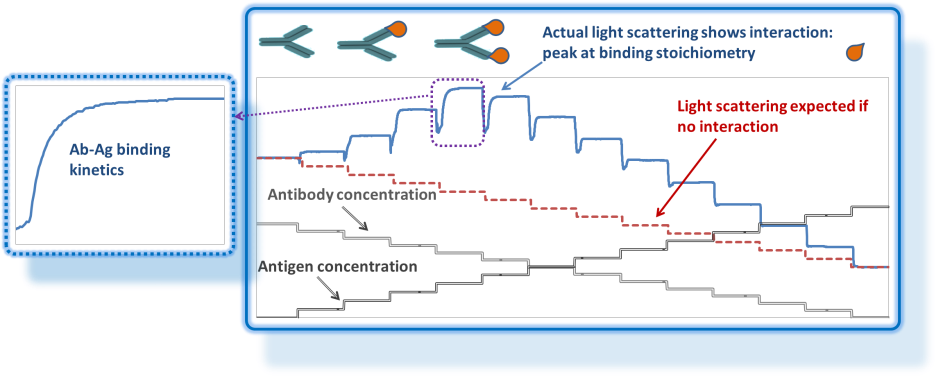
了解 CG-MALS
光散射不仅测量摩尔质量和分子尺寸- 它也是研究溶液中大分子相互作用而无需借助标记或固定化的绝佳工具。成分梯度多角度静态光散射(CG-MALS或CG-SLS)采用与色谱模式相同的检测器:多角度静态光散射检测器,并且通常与示差折光检测器或 UV / Vis 检测器结合使用。
CG-MALS 代替了连续流动的分馏设备提供的尺寸分离的样品,它利用了 Calypso™ 多注射器泵系统进行编程,以一系列明确定义的浓度或组分提供停流进样。在平衡后,分析在每个步骤获得的数据,以确定动态平衡性质:特定配合物的化学计量和结合亲和力(KA),或在非特异性相互作用的情况下,热力学参数(如维里系数)。还可以分析每种组合物的反应速率以确定动力学参数,例如 Michaelis 常数(kM)或缔合/解离速率常数(kon, koff)。
从概念上讲,CG-MALS 是完全基于第一原理和严格的热力学基础的绝对技术。由于静态光散射可测量重均摩尔质量,因此 CG-MALS 不仅提供化学计量比,而且还提供完整的复杂化学计量。可以量化经历自缔合、异缔合和甚至同时自缔合或异缔合的系统。 CG-MALS 的一项特殊优势是对元复合物的分析(例如,简单复合物的自缔合,例如反应A+B+A+B↔AB+AB↔(AB)2)。相互作用分析不仅限于大分子,还可以扩展到较大物体的行为,例如脂质体或微凝胶颗粒(包括粘附在此类物体上的大分子),并且同一仪器可以使其他现象的研究自动化,例如纳米颗粒降解动力学。
关于 CG-MALS 的理论和实践的其他细节,以及各种实例,可以在“通过静态和动态光散射表征蛋白质的相互作用”中找到。作者:Jianfeng Cai 和 Rongsheng Wang,InTech,2012。该出版物可在此处免费下载。
关于 CG-MALS 的理论和高级示例的另一个有价值的参考文献是“基于光散射的生物分子相互作用的分析”,可在此处免费下载。
以下部分介绍CG-MALS背后的理论:
在理想条件下的特异性结合
在理想或非常稀的条件下,可忽略热力学上的非理想性(例如,维里系数项),并且从包含一个或多个大分子的溶液中得到的时间 - 平均光散射强度由方程描述:
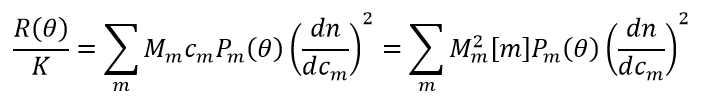
这里:
- Mm, cm, Pm(θ) 和 dn/dcm 是指摩尔质量,质量/体积浓度,有限rg引起的角度依赖性以及分子种类m的比折射率
- [m] 是物质 m 的摩尔浓度
- R(θ) 和 K 的定义与“经典散射/分析详细信息”中的定义相同,只是从K*中删除了dn/dc以产生与样本无关的参数K
对于具有合理离子强度的缓冲液中的大多数蛋白质,理想限值通常在总浓度低于〜1 mg / mL时有效。 对于其他大分子和溶剂,有效范围可能有所不同。
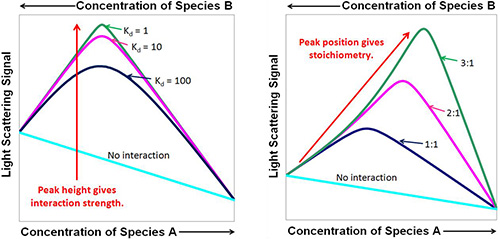
在此范围内,考虑动态平衡的可逆缔合体系由1)浓度为[A] 和 [B]的摩尔质量为MA 和 MB的游离单体A, B。2)在浓度[AiBj]下摩尔质量为Mij = iMA + jMB的结合配合物AiBj。按照Attri&Minton 20051提出的形式主义,数据分析包括将理想的光散射方程式(以下更写为(1))与质量作用方程式(2)和质量守恒方程式(3)结合在一起:
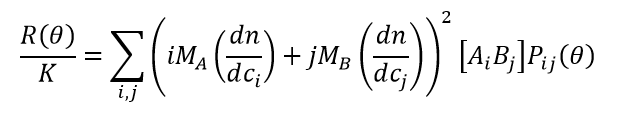 (1)
(1)
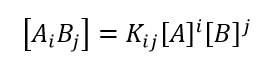 (2)
(2)
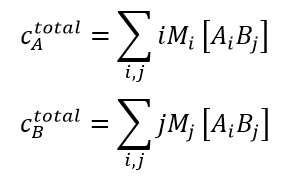 (3)
(3)
- 此处 A1B0 和 A0B1 代表 A 和 B 单体; AiB0 代表 A 的i-mers ,A0Bj 代表B的j-mers。
- 在等式中 (2),Kij是ij络合物的宏观平衡常数。
- 在等式中 (3),cAtotal 和 cBtotal是溶液中 A 和 B 的总质量/体积浓度。 通常这些由混合在一起以产生反应的量确定。 在许多情况下,在CG-MALS实验过程中直接测量cAtotal 和 cBtotal。
References
1 Attri, A. K.; Minton, A. P. Composition gradient static light scattering: A new technique for rapid detection and quantitative characterization of reversible macromolecular hetero-associations in solution. Analytical Biochemistry 2005, 346, 132–138.
非特异性相互作用或非理想性热力学
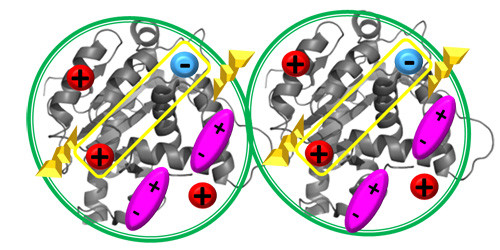 大分子间的非特异性相互作用有多种来源:硬核排斥、分子表面静电净电荷引起的排斥或吸引、各种偶极项和高阶项(单极偶极、偶极偶极等)引起的吸引、蛋白质或肽上的疏水斑、水化力等相互作用是由溶剂介导的,因此受到离子强度和pH值的影响。它们不会导致特定的、锁和键结合,从而产生具有明确化学计量比的配合物,而是在大分子之间产生整体吸引或排斥。在接近(但未达到)理想极限的相对稀释条件下,非特定的自相互作用可通过维里系数方便地量化,特别是第二维里系数A2(也称为 B22)和第三维里系数A3(B222)。在稀释的、非理想状态下的静态光散射方程通常是这样写的:
大分子间的非特异性相互作用有多种来源:硬核排斥、分子表面静电净电荷引起的排斥或吸引、各种偶极项和高阶项(单极偶极、偶极偶极等)引起的吸引、蛋白质或肽上的疏水斑、水化力等相互作用是由溶剂介导的,因此受到离子强度和pH值的影响。它们不会导致特定的、锁和键结合,从而产生具有明确化学计量比的配合物,而是在大分子之间产生整体吸引或排斥。在接近(但未达到)理想极限的相对稀释条件下,非特定的自相互作用可通过维里系数方便地量化,特别是第二维里系数A2(也称为 B22)和第三维里系数A3(B222)。在稀释的、非理想状态下的静态光散射方程通常是这样写的:
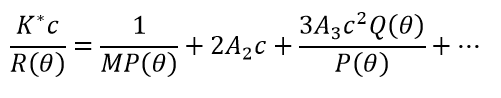 (4)
(4)
Or
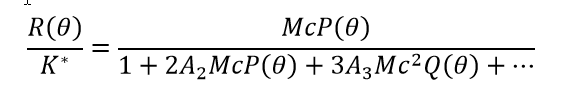 (5)
(5)
对于远小于入射光波长的分子,P(θ)=1 和 Q(θ)=1,通常半径小于8–10 nm。用交叉维里系数,特别是A11 (B23)可以方便地描述非特异性的异质相互作用。虽然有各种形式来描述具有自维里系数和交叉维里系数的光散射,但常用的变体是:
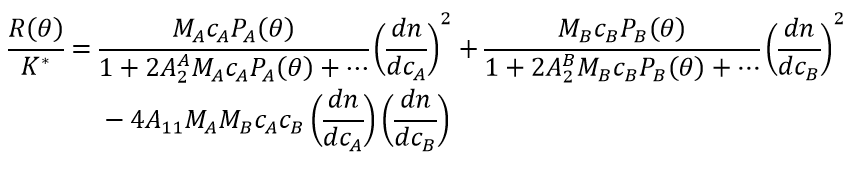 (6)
(6)
在这些方程式中,没有区分为化学计量的配合物。 >c,cA 和 cB是指总样品浓度。
高浓度分析:弱关联或准关联
在高浓度下(对于蛋白质和类似的大分子而言,通常高于10 mg / mL 且高达数百 mg / mL),不影响稀溶液或中等浓度溶液的弱相互作用可能变得很重要。在如此高的浓度下获得的 CG-MALS 数据的分析由于同时存在排斥相互作用(特别是总是存在的硬核排斥)和各种非特异性的吸引相互作用而变得复杂。幸运的是,排斥性和吸引性相互作用往往会在浓度依赖性上产生不同的功能形式,从而使它们能够被同时区分和定量。
有效硬球(EHS)模型通常可以很好地适应主要排斥反应产生的信号1。 EHS使用单个参数,即有效比容veff,可以从该参数计算出所有维里系数的阶数,从而使拟合过程更可靠。 外推至零角(或各向同性散射体(即半径小于8-10 nm的分子)以任意角度外推):
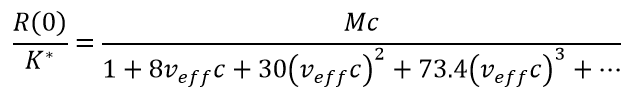 (7)
(7)
Minton 描述了一个分析高浓度自相互作用的框架,假设所有的吸引力都可以描述为可逆的聚合,而所有的排斥力都可以转化为一个单一的参数:有效比体积veff,对于单体和所有的“聚合物”阶数都是相等的。这些“低聚物”可能不是具有可靠化学计量比的真正的特定配合物,但可以认为是具有近似化学计量比的准特定低聚物,其化学计量比可能随着溶剂条件的改变而改变。将高浓度数据拟合到自缔合模型并确定化学计量比、i-mer平衡缔合常数Ki 和 veff的完整算法相当复杂。通过将等式(7)与等式(qs)结合,得到了一组高度简化的方程组,该方程组在存在(排斥)非理想性的情况下合理地复制了自缔合系统的本质。 (1)-(3):
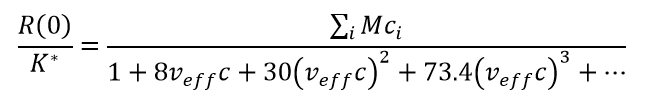 (8)
(8)
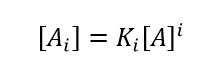 (9)
(9)
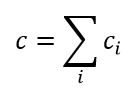 (10)
(10)
>References
1 Minton, A. P. Light Scattering from Concentrated Protein Solutions, I: General Theory for Protein Mixtures and Application to Self-Associating Proteins. Biophysical Journal 2007, 93, 1321-1328.
反应动力学
标准溶液反应动力学适用于光散射。 散射信号显然与浓度和摩尔质量的乘积有关,因此可通过一组相应的方程式描述数据。 对于A+B↔AB的简单情况,结果是二阶动力学:
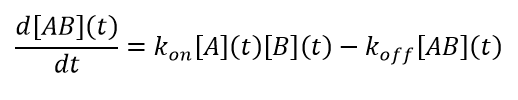 (11)
(11)
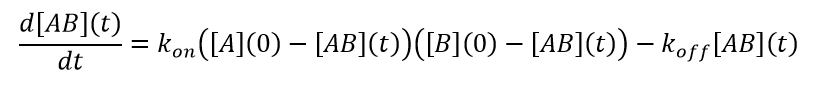 (12)
(12)
外推到零角度(或各向同性散射体(即半径 < 8-10 nm 的粒子)的任何角度)上的超瑞利比的时间依赖性为:
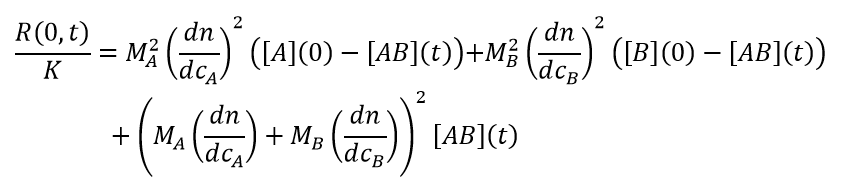 (13)
(13)