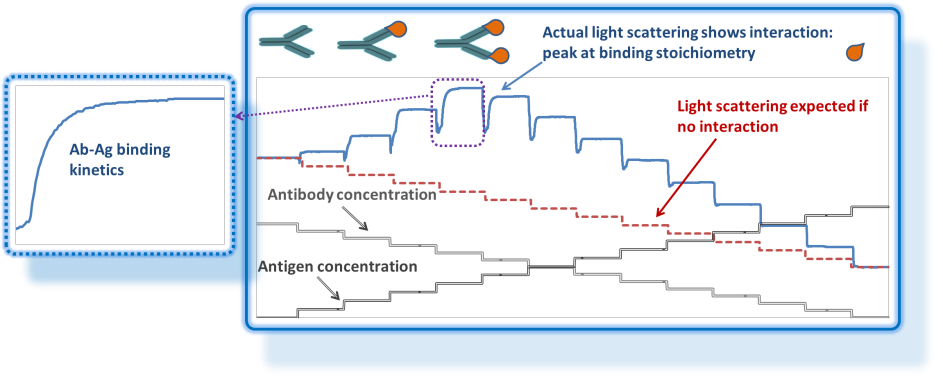
Understanding CG-MALS
Light scattering goes beyond molar mass and size – it is also a great tool for studying macromolecular interactions in solution without recourse to labeling or immobilization. Composition-Gradient Multi-Angle static Light Scattering (CG-MALS or CG-SLS) employs the same detectors used in chromatography mode: a multi-angle static light scattering photometer, often in combination with a differential refractometer or UV/Vis absorption spectrophotometer.
Instead of a continuously flowing fractionation apparatus to provide size-separated samples, CG-MALS utilizes the Calypso™ multi-syringe pump system, programmed to provide stop-flow injections at a series of well-defined concentrations or compositions. Data acquired at each step, after equilibration, is analyzed to determine dynamic equilibrium properties: the stoichiometry and binding affinity (KA) of specific complexes, and/or thermodynamic parameters such as virial coefficients in the case of non-specific interactions. The reaction rates at each composition may also be analyzed to determine kinetic parameters such as the Michaelis constant (kM) or association/dissociation rate constants (kon, koff).
Conceptually, CG-MALS is an absolute technique based entirely on first principles and a rigorous thermodynamic foundation. Since static light scattering measures weight-average molar mass, CG-MALS provides not only the stoichiometric ratio, but full complex stoichiometry. Systems undergoing self-interaction, hetero-association, or even simultaneous reversible self- and hetero-association may be quantified. A particular strength of CG-MALS is the analysis of metacomplexes (e.g., the self-association of simple complexes such as the reaction A+B+A+B↔AB+AB↔(AB)2). Interaction analysis is not limited to macromolecules but may be extended to the behaviour of larger objects such as liposomes or microgel particles (including macromolecules adhering to such objects), and the same instrumentation may serve to automate the study of additional phenomena such as nanoparticle degradation kinetics.
Additional details on the theory and practice of CG-MALS, as well as a variety of examples, may be found in "Characterization of Protein-Protein Interactions via Static and Dynamic Light Scattering", in Protein Interactions, ed. Jianfeng Cai and Rongsheng Wang, InTech, 2012. The publication is freely downloadable here.
Another valuable reference on theory and advanced examples of CG-MALS is "Light-scattering-based analysis of biomolecular interactions", available as an open access download here.
These sections contain a concise overview of the theory behind CG-MALS:
Specific binding in the ideal limit
In the ideal, or very dilute, limit, thermodynamic non-ideality (e.g., virial coefficient terms) may be ignored and the time-averaged light scattering intensity from a solution containing one or more macromolecules is described by the following equation:
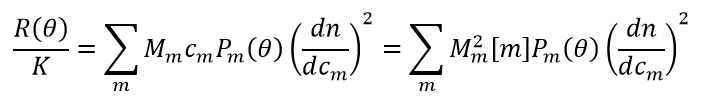
In this equation:
- Mm, cm, Pm(θ) and dn/dcm refer to the molar mass, mass/volume concentration, angular dependence due to finite rg, and specific refractive index of molecular species m
- [m] is the molar concentration of species m
- R(θ) and K are defined as in Classical Scattering/Analysis Details, except that dn/dc is removed from K* to produce a sample-independent parameter K
The ideal limit is typically valid below ~1 mg/mL total concentration for most proteins in buffer of reasonable ionic strength. For other macromolecules and solvents the range of validity may vary.
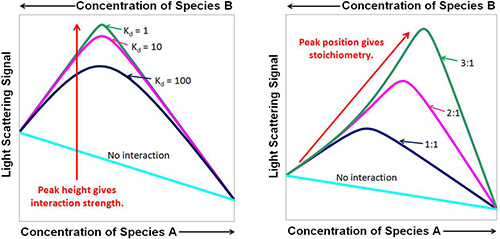
Within this limit, a reversibly associating system in dynamic equilibrium is considered to consist of a mixture of 1) free monomers A, B of molar masses MA and MB at concentrations [A] and [B]; and 2) bound complexes AiBj of molar mass Mij = iMA + jMB at concentrations [AiBj]. Following the formalism laid out by Attri & Minton 20051, data analysis consists of combining the ideal light scattering equation, rewritten here as (1), with the equations for mass action (2) and conservation of mass (3).
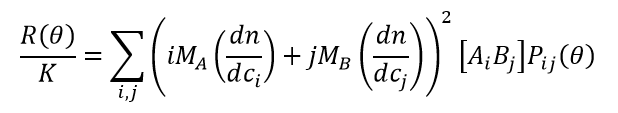 (1)
(1)
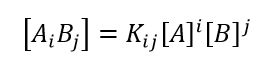 (2)
(2)
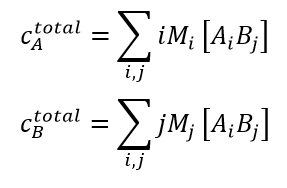 (3)
(3)
- Here A1B0 and A0B1 represent A and B monomers; AiB0 represents i-mers of A and A0Bj represents j-mers of B.
- In Eq. (2), Kij are the macroscopic equilibrium constants for the ij complex
- In Eq. (3), cAtotal and cBtotal are the total mass/volume concentration of A and B present in solution. Usually these are determined from the amounts mixed together to produce the reaction. In many cases cAtotal and cBtotal are measured directly in the course of a CG-MALS experiment.
References
1 Attri, A. K.; Minton, A. P. Composition gradient static light scattering: A new technique for rapid detection and quantitative characterization of reversible macromolecular hetero-associations in solution. Analytical Biochemistry 2005, 346, 132–138.
Non-specific interactions, or thermodynamic non-ideality
Non-specific interactions between macromolecules arise from a variety of sources: hard-core repulsion, repulsion or attraction due electrostatic net charges on molecular surfaces, attraction due to various dipole and higher-order terms (monopole-dipole, dipole-dipole, etc.), hydrophobic patches on proteins or peptides, hydration forces, etc. Such interactions are mediated by the solvent and hence affected by ionic strength and pH. They do not result in specific, lock-and-key binding to produce complexes of well-defined stoichiometry, rather generate an overall attraction or repulsion between macromolecules.
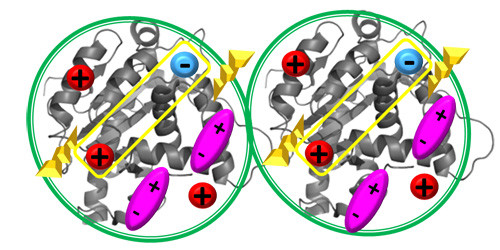
Under relatively dilute conditions that approach (but do not reach) the ideal limit, non-specific self-interactions are conveniently quantified by virial coefficients, especially the second virial coefficient A2 (also known as B22) and the third virial coefficient A3 (B222). The static light scattering equation in the dilute, non-ideal regime is usually written as:
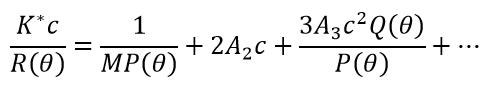 (4)
(4)
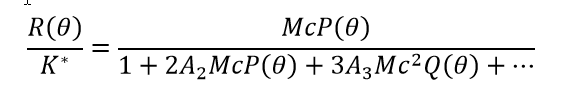 (5)
(5)
Both P(θ)=1 and Q(θ)=1 for molecules much smaller than the wavelength of incident light, typically with radii < 8–10 nm. Non-specific hetero-interactions are conveniently described by cross-virial coefficients, especially A11 (B23). While there are various formalisms to describe light scattering with self-and cross-virial coefficients, a commonly-used variant is seen in equation 6.
In these equations, there is no differentiation into stoichiometric complexes; >c, cA and cB refer to total sample concentrations.
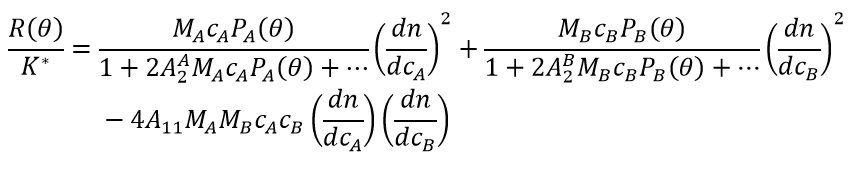 (6)
(6)
High-concentration analysis: weak or quasi-specific associations
At high concentrations, typically above 10 mg/mL and up to hundreds of mg/mL for proteins and similar macromolecules, weak interactions that do not affect dilute or moderately concentrated solutions may become important. The analysis of CG-MALS data acquired at such high concentration is complicated by the simultaneous presence of repulsive interactions (especially hard-core repulsion which is always present) and a variety of non-specific, attractive interactions. Fortunately, repulsive and attractive interactions tend to produce different functional forms in their concentration dependence, permitting them to be distinguished and quantified simultaneously.
Signals from a primarily repulsive interaction are often fit well by the Effective Hard Sphere (EHS) model1. EHS utilizes a single parameter, the effective specific volume veff, from which all orders of virial coefficients may be calculated, making the fitting procedure robust. Extrapolating to zero angle (or at any angle for isotropic scatterers (i.e., molecules with radius below 8-10 nm) as seen in equation 7.
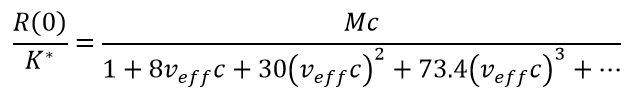 (7)
(7)
Minton described a framework for analysing high-concentration self-interactions by assuming that all the attraction can be described as reversible oligomerization, while all the repulsion can be rolled into a single parameter: the effective specific volume veff which is held to be equal for monomers and all orders of 'oligomers'. These 'oligomers' may not be true specific complexes with robust stoichiometries, but can be thought of as quasi-specific oligomers with approximate stoichiometries that may shift upon changing solvent conditions. The complete algorithm to fit high-concentration data to a self-association model and determine stoichiometry, i-mer equilibrium association constants Ki and veff is rather involved. A highly simplified set of equations which does a reasonable job of replicating the essentials of a self-associating system in the presence of (repulsive) non-ideality is obtained by combining Eq. (7) with Eqs. (1) - (3).
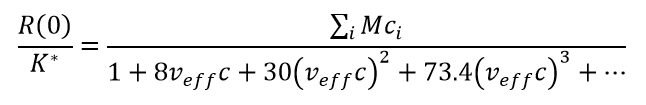 (8)
(8)
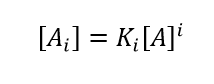 (9)
(9)
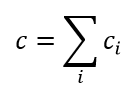 (10)
(10)
References
1 Minton, A. P. Light Scattering from Concentrated Protein Solutions, I: General Theory for Protein Mixtures and Application to Self-Associating Proteins. Biophysical Journal 2007, 93, 1321-1328.
Reaction kinetics
Standard solution reaction kinetics apply to light scattering. The scattering signal is of course related to the product of concentration and molar mass, so that the data will be described by a corresponding set of equations. For the simple case of A+B↔AB, the result is 2nd order kinetics:
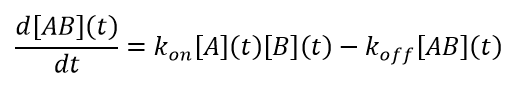 (11)
(11)
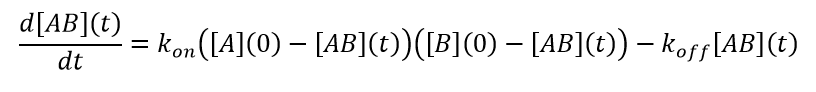 (12)
(12)
The time dependence of the excess Rayleigh ratio, extrapolated to zero angle (or at any angle for isotropic scatterers (i.e., particles of radius < 8–10 nm), is:
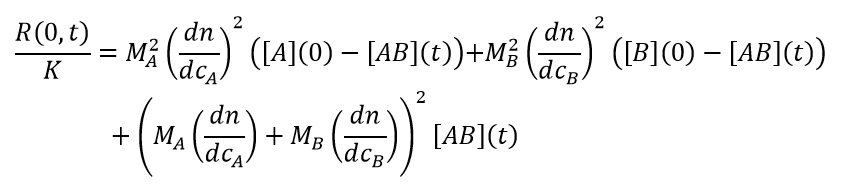 (13)
(13)