Understanding Multi-Angle Static Light Scattering
In the 19th century, Lord Rayleigh (John William Strutt) offered the first explanation for the sky's brilliant blue color (on a clear day!). His insights were based on the fundamental equations describing light and its interaction with matter, laid out by James Clerk Maxwell in 1865 in one of the most important achievements of theoretical physics. The extension of Rayleigh’s theory to describe the scattering of light by larger macromolecules in solution is called the Rayleigh-Gans-Debye (RGD) theory of light scattering.
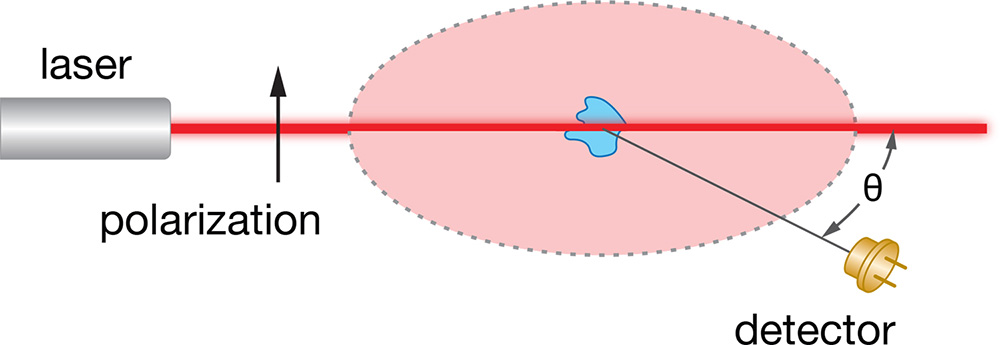
In a typical light scattering experiment, a well collimated, single frequency, polarized light beam (i.e., from a laser) is used to illuminate a solution containing a suspension of the macromolecules or nanoparticles of interest. The electric field of the polarized light beam is preferably produced perpendicular to the plane in which the intensity and angular dependence of the subsequently scattered light is to be measured (by convention, the polarization direction is denoted ‘vertical’ and the measurement plane ‘horizontal’) . The overall intensity carries information about the molar mass, while the angular dependence within the horizontal plane carries information about the size of the macromolecule.
The following theory section contains a brief overview of the following topics related to multi-angle light scattering:

Intensity and Molar Mass
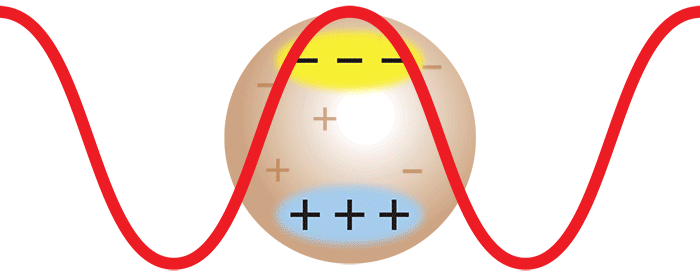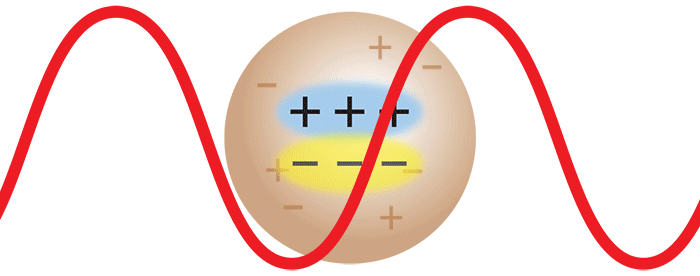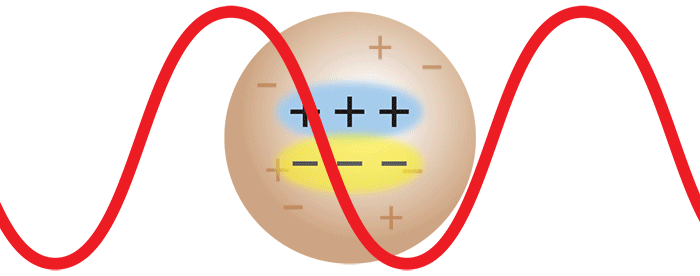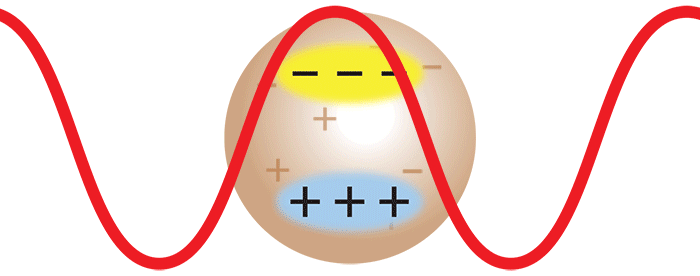
When laser light impinges on a macromolecule, the oscillating electric field of the light induces an oscillating dipole within it. This oscillating dipole will re-radiate light, much like the antenna for a radio station sends out radio waves. The intensity of the radiated light depends on the magnitude of the dipole induced in the macromolecule. The more polarizable the macromolecule, the larger the induced dipole, and hence, the greater the intensity of the scattered light. Therefore, in order to analyze the scattering from a solution of such macromolecules, it is necessary to know their polarizability relative to the surrounding medium (i.e., the solvent). This may be determined from a measurement of the change, Δn, of the solution's refractive index n with the molecular concentration change, Δc, by measuring the dn/dc (=Δn/Δc) value using an Optilab™ differential refractometer.
When there are many macromolecules in solution, each macromolecule scatters light via the aforementioned induced dipole mechanism. Hence, the intensity of the scattered light is proportional to the concentration of the macromolecules in solution; twice as many molecules scatter twice as much light.
Consider now the important case where two monomers aggregate to form a dimer in solution. The initially separate monomers are constantly buffeted by solvent molecules, and undergo random motion known as Brownian motion. This imparts a randomness to the phase of the scattered light such that the light from the two separate monomers is incoherent. Averaged over time, the scattered intensities add as one expects classically: 1 + 1 = 2.
However, once the monomers form a dimer, the two monomers move together. The scattered light from one monomer now has a definite phase relationship with the scattered light from the other. In other words, the scattering is coherent. The net result is that the scattered light from the dimer is twice as intense as the total light scattered from two independent monomers. Simply by doubling the molar mass, even while keeping the mass/volume concentration the same, the intensity of the scattered light doubles. The intensity of light scattered by a molecule, measured by means of a DAWN™ or miniDAWN™ multi-angle light scattering (MALS) detector, is directly proportional to the molar mass. Light scattering thus represents a powerful technique for determining the molar mass of macromolecules in solution as well as monitoring the presence and formation of aggregates.
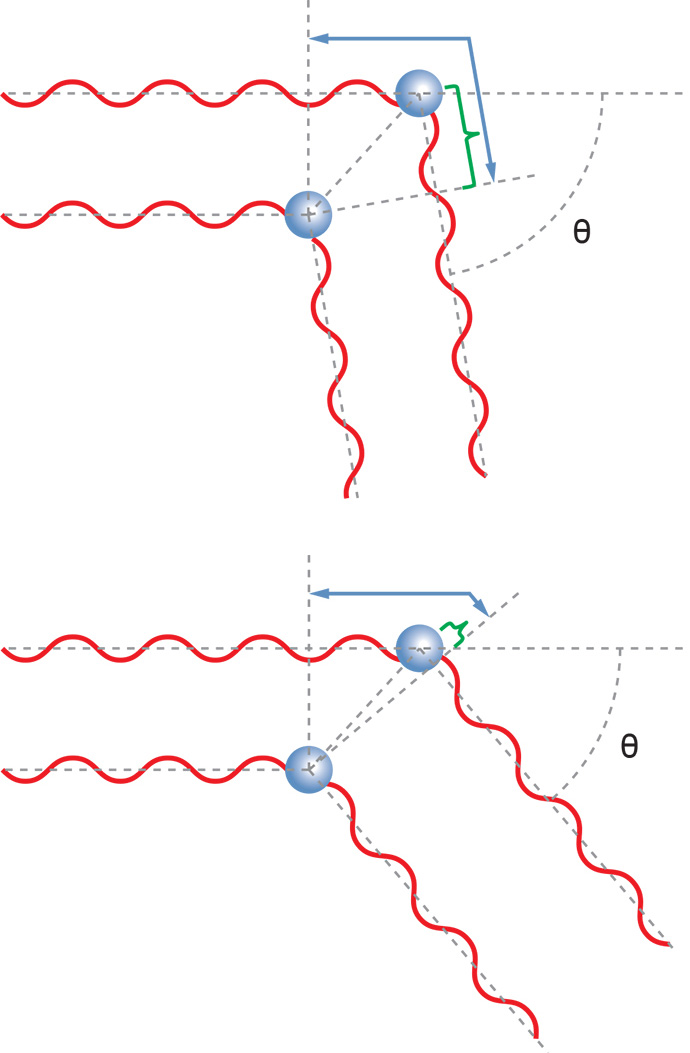
Angular Dependence and Size
Macromolecules much smaller than the wavelength of the incident light can be treated as though they were essentially point scatterers. For such very small molecules, the light scattered into the perpendicular plane is independent of scattering angle. It is the same at every scattering angle – the macromolecule scatters light isotropically.
For larger macromolecules, light scattered from different parts of the macromolecule reach the detector with different phases. This can lead to the destructive or constructive interference of the overall light wave at the detector. The net result is that the intensity of light scattered away from the direction of propagation of the laser beam is reduced relative to light scattered into the forward direction, and in fact varies with angle. This case is described by the RGD theory mentioned earlier.
If the angular dependence of the scattered light is measured in the horizontal plane, it is possible to determine the size of the molecule. This size measurement is known as the root mean square (rms) radius, or sometimes the "radius of gyration," Rg. The rms radius is a measure of the molecule's size weighted by the mass distribution about its center of mass. If the molecule's conformation is determined to belong to a specific class (e.g., random coil, sphere, or rod), the rms radius can be related to its geometrical dimensions. A sample containing a broad distribution of molecular masses may be separated by SEC or GPC, and light scattering data acquired at each elution volume to determine molar mass Mw and Rg. The measured rms radius may be plotted against the correspondingly measured molar mass to determine the sample's conformation.
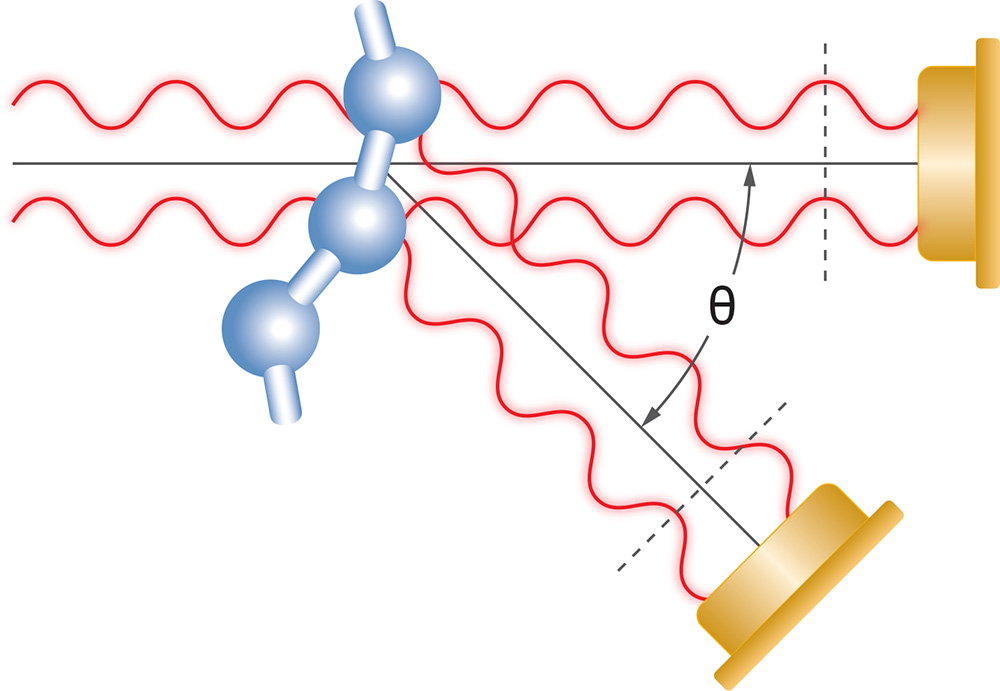
Particle Concentration
Taking advantage of the determination of size from the angular dependence of the scattered light, and the total scattered intensity, another important property can be measured: the concentration of nanoparticles, N.
The calculation requires the particle’s volume V and refractive index nparticle, and the refractive index of the solvent n0. The assumption of a specific shape such as sphere or rod is required. Then the equation corresponding to the shape may be fit to the angular data to obtain a dimension such as radius or length, from which the volume of the particle is calculated. The refractive index of the particle’s constituent material may be found in the literature. The angular data must be extrapolated to angle zero in order to evaluate the particle concentration.
If a particle does not consist of a homogeneous material then the refractive index value used should be the weight-average refractive index nw of the entire volume of the particle. For example, nparticle of an enveloped virus would be the weight-average of the n values of the protein, nucleic acids and glycans. For an empty liposome the solvent content in the core should be accounted for.
To learn more visit the particle concentration page.
Equations and Data Analysis
The theoretical foundation laid out by Bruno Zimm1 makes it possible to condense the results of the Rayleigh-Debye-Gans theory of light scattering into a simple equation. As described in the review article by Philip Wyatt in 19932, Zimm's development leads to the following expression:
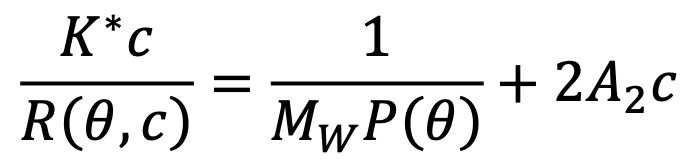
In this expression:
- R(θ,c) is the excess Rayleigh ratio of the solution as a function of scattering angle θ and concentration c. It is directly proportional to the intensity of the scattered light in excess of the light scattered by the pure solvent.
- c is the solute concentration.
- Mw is the weight-averaged solute molar mass.
- A2 is the second virial coefficient in the virial expansion of the osmotic pressure.
- K* is the constant 4π2(dn/dc)2n02/Naλ04.
- Na is Avogadro's number. This number always appears when concentration is measured in g/mL and molar mass in g/mol.
- P(θ) describes the angular dependence of the scattered light, and can be related to the rms radius.
The expansion of P(θ) to first order gives:
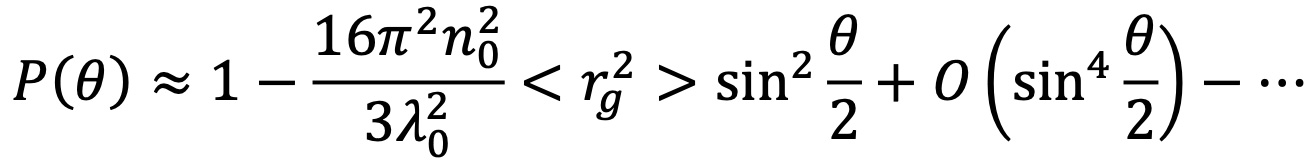
In this expression, n0 is the index of refraction of the solvent, λ0 is the vacuum wavelength of the laser, and Rg is the rms radius. Here, the relation between the size and angular dependence of the scattered light is clear. For larger sizes (Rg greater than approximately 50 nm) it is necessary to include higher moments in the expansion of P(θ).
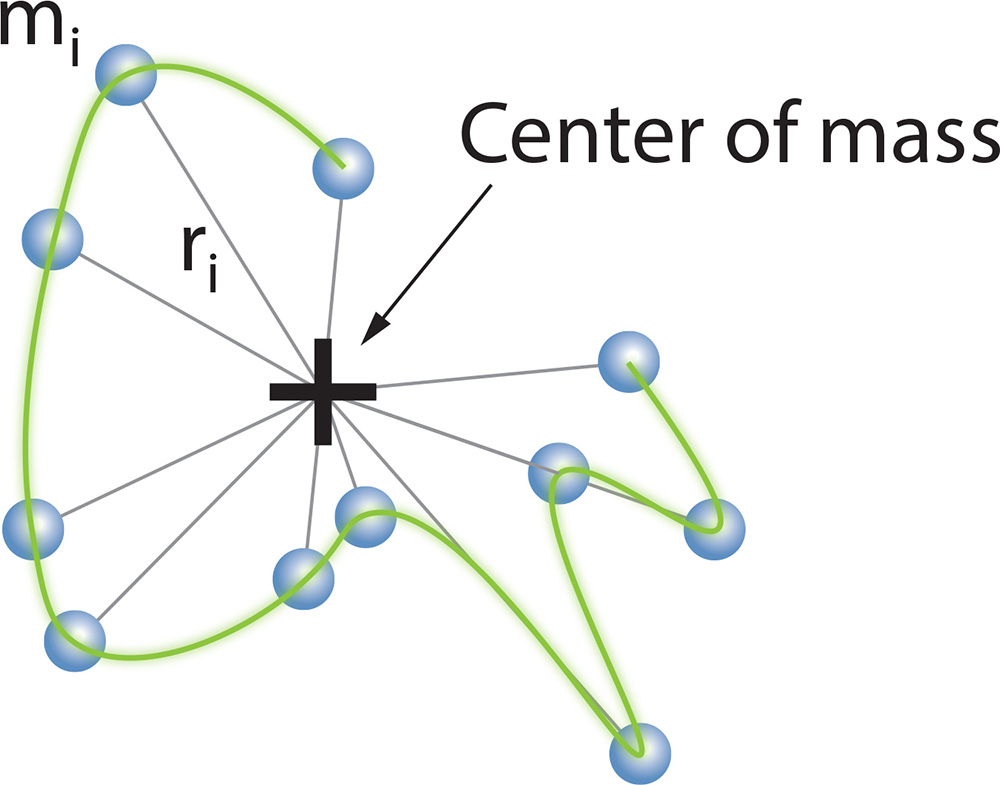
The mean square radius, <rg2>, may be calculated immediately from the slope at θ = 0 of the measured ratios 1/R(θ,c) with respect to sin2(θ/2). If the macromoledule of mass M is made up of elements mi, it may be shown that:
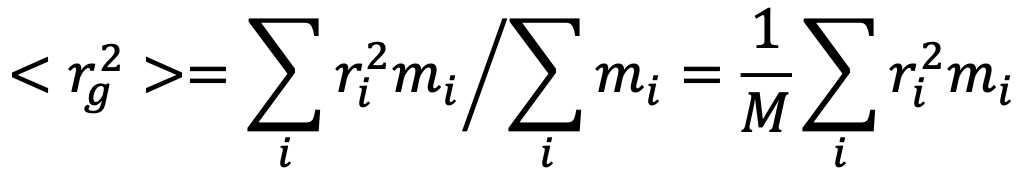
where ri is the distance of element mi from the center of mass of the molecule of total mass M.
The basic light scattering equation holds true at ALL angles, not just one! With modern computers we collect all of the angular data and apply a Global Fit, since the relationship between mass, size, and the quantities measured is valid at all angles. The so-called 'extrapolation' (to which some light scattering vendors may refer) actually consists of collecting a complete set of independent data points and using this full view of the scattering pattern to find the most accurate value of the molar mass, size and conformation. Wyatt performs, therefore, 18 simultaneous measurements with our 18-angle DAWN instrument.
Combining data obtained from more angles means greatly improved accuracy and precision. Nevertheless, some will argue that a measurement at a single low angle (in fact, the noisiest possible location!) is superior to a measurement over a range of angles. Clearly this argument is incorrect, as may be confirmed by the governing equations.
References
1 Zimm, B. H. The scattering of light and the radial distribution function of high polymer solutions. Journal of Chemical Physics 16, 1093-1099 Ibid. Apparatus and methods for measurement and interpretation of the angular variation of light scattering; Preliminary results on polystyrene solutions. Journal of Chemical Physics 1948, 16, 1099-1116.
2 Wyatt, P. J. Light scattering and the absolute characterization of macromolecules. Analytica Chimica Acta 1993, 272, 1–40.
For more information about Light Scattering and Chromatography Mode, please click here.
For more information about Light Scattering and Batch Mode, please click here.
