Die Grundlagen der Mehrwinkel Statischen Lichtstreuung
Im 19. Jahrhundert lieferte Lord Rayleigh (John William Strutt) die erste Erklärung für die strahlend blaue Farbe des Himmels (an einem klaren Tag!). Seine Erkenntnisse basierten auf den grundlegenden Gleichungen zur Beschreibung des Lichts und seiner Wechselwirkung mit der Materie, die James Clerk Maxwell 1865 als eine der wichtigsten Errungenschaften der theoretischen Physik aufstellte. Die Erweiterung von Rayleighs Theorie zur Beschreibung der Streuung von Licht an größeren Makromolekülen in Lösung wird als Rayleigh-Gans-Debye (RGD) Theorie der Lichtstreuung bezeichnet.
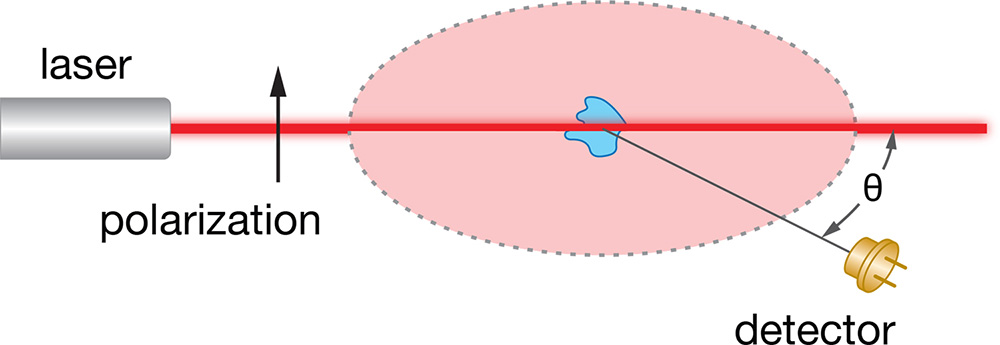
In einem typischen Lichtstreuexperiment wird ein gut kollimierter, polarisierter, mono-chromatischer Lichtstrahl (z. B. von einem Laser) verwendet, um die Suspension der Makromoleküle oder Nanopartikel zu beleuchten. Das elektrische Feld des polarisierten Lichtstrahls wirkt vorzugsweise senkrecht zu der Ebene, in der Intensität und Winkelabhängigkeit des gestreuten Lichts gemessen werden soll (die Polarisationsrichtung wird als "vertikal" und die Messebene als "horizontal" bezeichnet). Die Gesamtintensität des gestreuten Lichtes enthält Informationen über die molare Masse, während die Winkelabhängigkeit des gestreuten Lichtes Informationen über die Größe des Makromoleküls enthält.
Der folgende Theorieteil enthält einen kurzen Überblick über die folgenden Themen im Zusammenhang mit der Mehrwinkel-Lichtstreuung:

Intensität des Streulichtes und Molare Masse
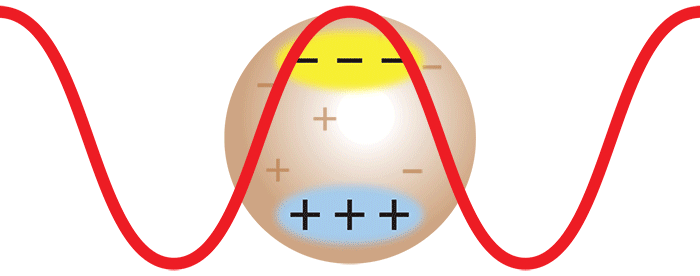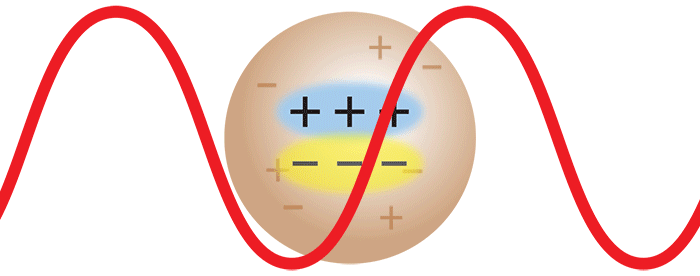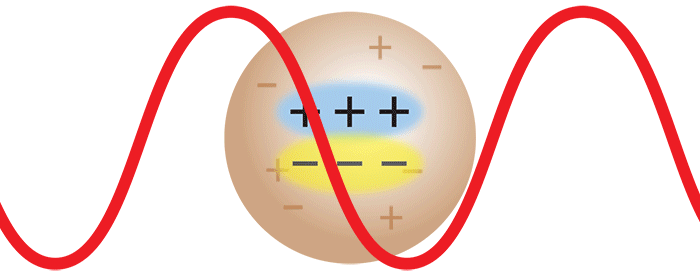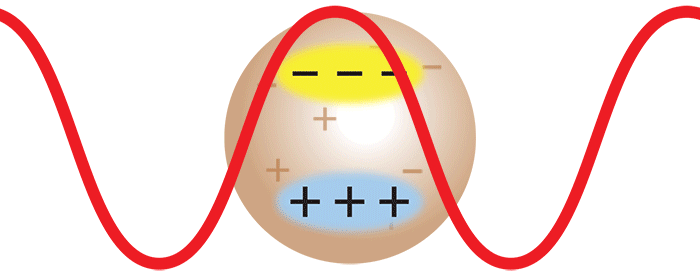
Wenn Laserlicht auf ein Makromolekül auftrifft, induziert das oszillierende elektrische Feld des Lichts einen oszillierenden Dipol in dem Makromolekül. Dieser oszillierende Dipol emittiert Licht, ähnlich wie die Antenne eines Radiosenders Radiowellen aussendet. Die Intensität des emittierten Lichtes hängt von der Stärke des im Makromolekül induzierten Dipols ab. Je stärker polarisierbar das Makromolekül ist, desto größer ist der induzierte Dipol und damit auch die Intensität des gestreuten Lichts. Um die Streuung aus einer Lösung solcher Makromoleküle analysieren zu können, muss man ihre Polarisierbarkeit relativ zum umgebenden Medium (d. h. dem Lösungsmittel) kennen. Diese kann durch eine Messung der Änderung Δn des Brechungsindex n der Lösung mit der Änderung der Molekülkonzentration Δc bestimmt werden, indem der Wert dn/dc (=Δn/Δc) mit einem Optilab® Differenzialrefraktometer gemessen wird.
Wenn sich viele Makromoleküle in Lösung befinden, streut jedes Makromolekül das Licht über den oben erwähnten induzierten Dipolmechanismus. Daher ist die Intensität des gestreuten Lichts proportional zur Konzentration der Makromoleküle in Lösung; doppelt so viele Moleküle streuen doppelt so viel Licht.
Betrachten wir nun den wichtigen Fall, dass zwei Monomere in Lösung zu einem Dimer aggregieren. Die ursprünglich getrennten Monomere unterliegen einer Zufallsbewegung, die als Brownsche Molekularbewegung bekannt ist. Dies verleiht der Phase des gestreuten Lichts eine Zufälligkeit, so dass das Licht der beiden getrennten Monomere inkohärent ist. Über die Zeit gemittelt, addieren sich die Intensität des Streulichtes der zwei Monomere, wie man es klassischerweise erwartet: 1 + 1 = 2.
Sobald die zwei Monomere jedoch ein Dimer bilden, bewegen sich die beiden Monomere zusammen, in Phase. Das Streulicht des einen Monomers hat nun eine eindeutige Phasenbeziehung zum Streulicht des anderen. Mit anderen Worten, die Streuung ist kohärent. Das Ergebnis ist, dass das Streulicht des Dimers doppelt so intensiv ist wie das gesamte Streulicht von zwei unabhängigen Monomeren. Allein durch die Verdoppelung der molaren Masse, auch bei gleichbleibender Masse/Volumenkonzentration, verdoppelt sich die Intensität des gestreuten Lichts. Die Intensität des von einem Molekül gestreuten Lichts, gemessen mit einem DAWN® oder miniDAWN® Mehrwinkel-Lichtstreudetektor (MALS), ist direkt proportional zur molaren Masse. Die Lichtstreuung stellt somit eine leistungsfähige Technik zur Bestimmung der molaren Masse von Makromolekülen in Lösung sowie zur Überwachung des Vorhandenseins und der Bildung von Aggregaten dar.
Die Winkelabhängigkeit und die Größe
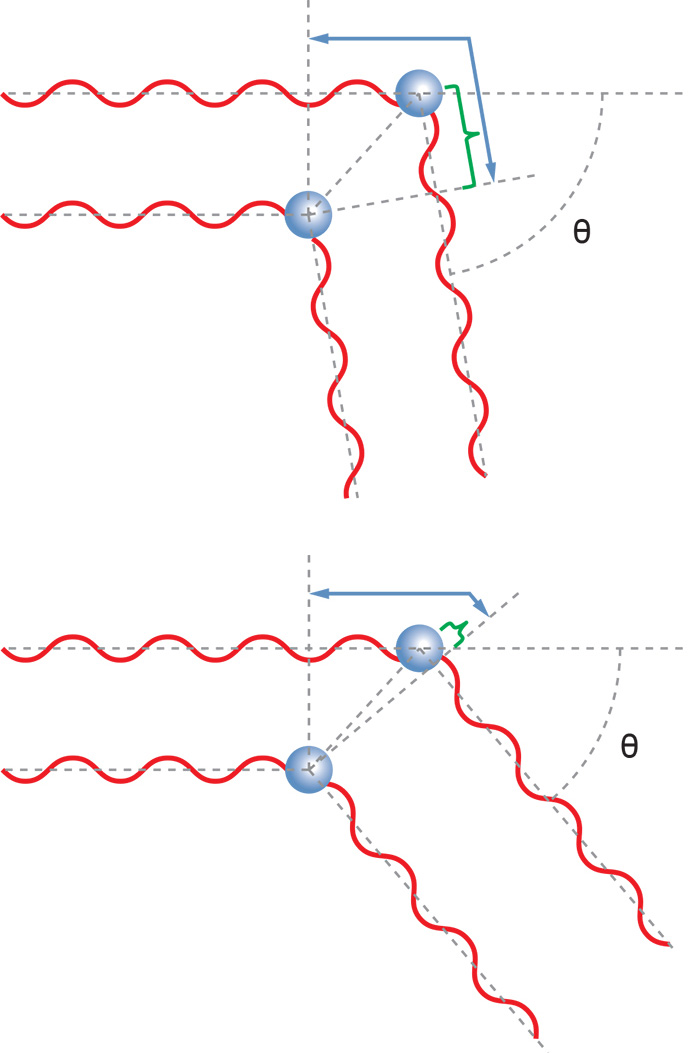
Makromoleküle, die viel kleiner als die Wellenlänge des einfallenden Lichts sind, können so behandelt werden, als wären sie im Wesentlichen punktförmige Streuzentren. Für solche sehr kleinen Moleküle ist das in die senkrechte Ebene gestreute Licht unabhängig vom Streuwinkel. Es ist bei jedem Streuwinkel gleich - das Makromolekül streut das Licht isotrop.
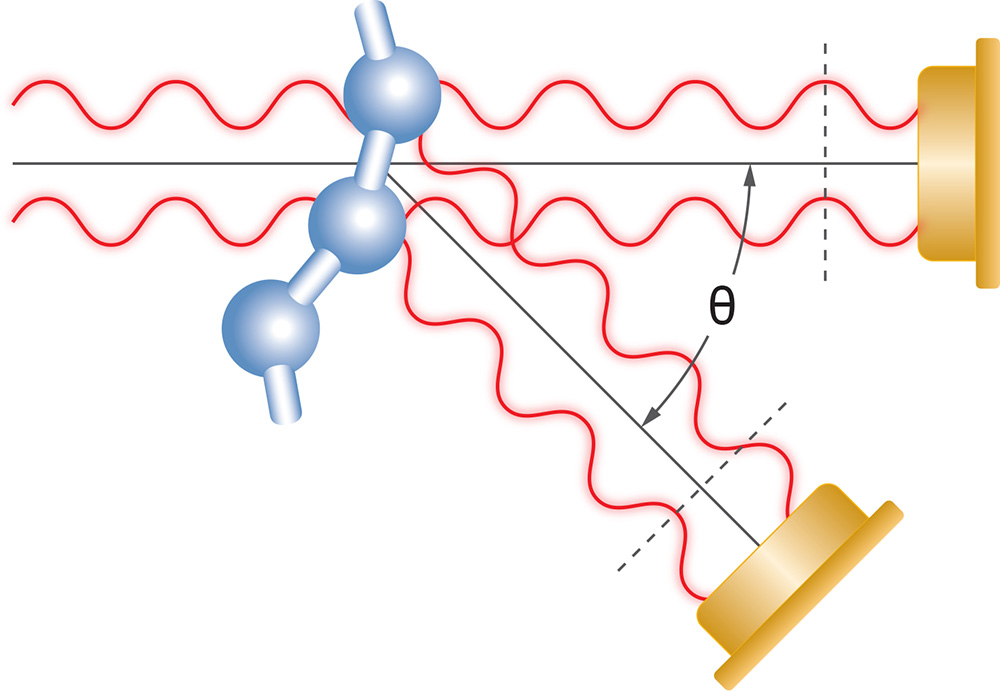
Bei größeren Makromolekülen erreicht das von verschiedenen Teilen des Makromoleküls gestreute Licht den Detektor mit unterschiedlichen Phasen. Dies kann zu einer destruktiven oder konstruktiven Interferenz der gesamten Lichtwelle am Detektor führen. Das Ergebnis ist, dass die Intensität des von der Ausbreitungsrichtung des Laserstrahls weggestreuten Lichts relativ zu dem in Vorwärtsrichtung gestreuten Licht reduziert ist und sogar mit dem Winkel variiert. Dieser Fall wird durch die bereits erwähnte RGD-Theorie beschrieben.
Misst man die Winkelabhängigkeit des Streulichts in der horizontalen Ebene, so ist es möglich, die Größe des Moleküls zu bestimmen. Diese Größe wird als „root mean square“ (rms) Radius oder manchmal auch als Gyrationsradius (radius of gyration, Rg), bezeichnet. Der rms-Radius ist ein Maß für die Größe des Moleküls, gewichtet mit der Massenverteilung um seinen Massenschwerpunkt. Wenn die Konformation des Moleküls bekannt ist (z. B. statistisches Knäuel, Kugel oder Stäbchen), kann der rms-Radius auf seine geometrischen Abmessungen bezogen werden. Eine Probe, die eine breite Verteilung von Molekülmassen enthält, kann durch SEC oder GPC aufgetrennt werden um die Lichtstreumessung bei jedem Elutionsvolumen durchzuführen, um also die molare Masse Mw und Rg zu bestimmen. Der gemessene rms-Radius (gemessen mit MALS) kann gegen die molare Masse (gemessen mit MALS) aufgetragen werden, um die Konformation der Probe mit Lichtstreuung zu bestimmen.
Partikel Konzentration
Durch das Bestimmen der Größe, berechnet aus der Winkelabhängigkeit des gestreuten Lichts und der Gesamtstreuintensität, kann eine weitere wichtige Eigenschaft gemessen werden: die Anzahl der Nanopartikel pro Volumeneinheit, N.
Für die Berechnung werden das Volumen V und der Brechungsindex nparticle der Partikel sowie der Brechungsindex n0 des Lösungsmittels benötigt. Die Annahme einer bestimmten Form wie Kugel oder Stab ist erforderlich, um die entsprechende Lichtstreufunktion zu verwenden. Mit Hilfe dieser Funktion werden die Winkeldaten angepasst, um über die Steigung den Radius zu ermitteln oder die Länge zu erhalten, aus der das Volumen des Teilchens berechnet wird. Der Brechungsindex des Materials, aus dem das Teilchen besteht, kann in der Literatur nachgeschlagen werden. Die Extrapolation auf den Winkel null mit Hilfe der gefitteten Winkeldaten ist proportional zur Anzahl der Partikel.
Besteht ein Partikel nicht aus einem homogenen Material, sollte als Brechungsindexwert der gewichtsgemittelte Brechungsindex nw des gesamten Volumens des Partikels verwendet werden. Zum Beispiel wäre nparticle eines umhüllten Virus das Gewichtsmittel der n-Werte des Proteins, der Nukleinsäuren und der Polysaccharide. Bei einem leeren Liposom sollte der Lösungsmittelgehalt im Kern berücksichtigt werden.
Weitere Informationen finden Sie auf der Seite Partikelkonzentration.
Gleichungen und Auswertungen
Die von Bruno Zimm1 gelegte theoretische Grundlage ermöglicht es, die Ergebnisse der Rayleigh-Debye-Gans-Theorie in einer einfachen Gleichung zusammenzufassen. Wie in dem Übersichtsartikel von Philip Wyatt aus dem Jahr 19932 beschrieben, führt Zimms Entwicklung zu der Gleichung:
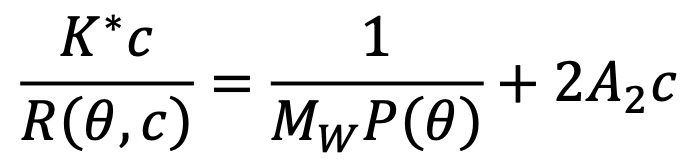
wobei:
- R(θ,c) ist das Excess-Rayleigh-Ratio der Lösung als Funktion des Streuwinkels θ und der Konzentration c. Es ist direkt proportional zur Intensität des gestreuten Lichts der Lösung im Vergleich zu der Intensität des gestreuten Lichts vom reinen Lösungsmittel.
- c ist die Konzentration des gelösten Stoffes.
- Mw ist die gewichtsgemittelte molare Masse des gelösten Stoffes.
- A2 ist der zweite Virialkoeffizient in der Virialerweiterung des osmotischen Drucks.
- K* ist die Lichtstreukonstante 4π2(dn/dc)2n02/Naλ04.
- Na ist die Avogadrosche Zahl. Diese Zahl ist immer dann erforderlich, wenn die Konzentration in g/mL und die molare Masse in g/mol gemessen wird.
- P(θ) beschreibt die Winkelabhängigkeit des gestreuten Lichts und kann mit dem rms-Radius in Beziehung gesetzt werden.
Die Erweiterung von P(θ) zur ersten Ordnung ergibt:
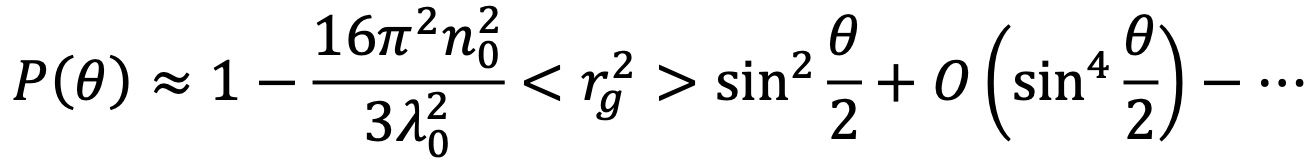
wobei n0 der Brechungsindex des Lösungsmittels, λ0 die Wellenlänge des Lasers im Vakuum und Rg der Gyrationsradius ist. Hier wird der Zusammenhang zwischen der Größe des Moleküls und der Winkelabhängigkeit des Streulichts deutlich. Für größere Größen (Rg größer als ca. 50 nm) ist es notwendig, höhere Momente in die Gleichung von P(θ) aufzunehmen.
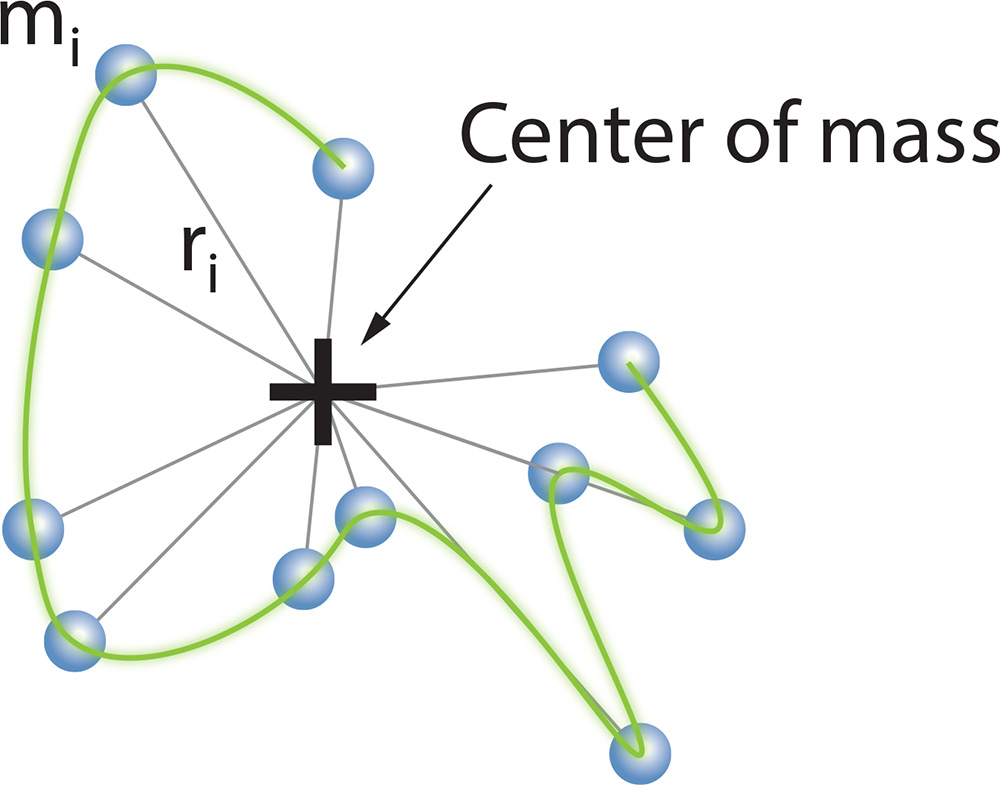
Der mittlere quadratische Radius, <rg2>, kann unmittelbar aus der Steigung beim Streuwinkel θ = 0 in der Auftragung von 1/R(θ,c) gegen sin2(θ/2) berechnet werden. Wenn die Makromoleküle der Masse M aus Elementen mi zusammengesetzt sind, kann gezeigt werden, dass
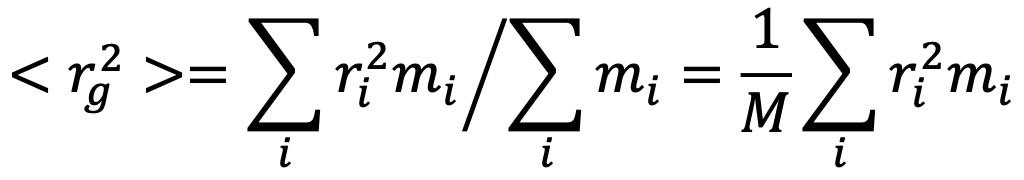
wobei ri der Abstand des Elements mi vom Massenschwerpunkt des Moleküls der Gesamtmasse M ist.
Die grundlegende Lichtstreuungsgleichung gilt für ALLE Winkel, nicht nur für einen! Mit dem Computer messen wir alle Winkeldaten simultan und wenden einen globalen Fit an, da die Beziehung zwischen Molmasse, Gyrationsradius und den gemessenen Rayleigh-Ratio unter allen Winkeln gültig ist. Die so genannte "Extrapolation" (auf die sich einige Anbieter von Lichtstreuung beziehen) besteht in Wirklichkeit darin, einen kompletten Satz unabhängiger Datenpunkte zu sammeln und diese vollständige Ansicht des Streumusters zu verwenden, um den genauesten Wert für Molmasse, Gyrationsradius und Konformation zu finden. Wyatt führt daher 18 simultane Messungen mit unserem 18-Winkel DAWN Instrument durch.
Die Kombination der gemessenen Streulichtintensitäten bei mehreren Winkeln bedeutet eine deutlich verbesserte Genauigkeit und Präzision. Dennoch werden einige argumentieren, dass eine Messung unter einem einzigen niedrigen Winkel (es in der Tat der, der am stärksten verrauschte Messwert liefert!) einer Messung über eine Reihe von Winkeln überlegen ist. Dieses Argument ist eindeutig falsch, was durch die maßgeblichen Gleichungen bestätigt werden kann.
Literatur
1 Zimm, B. H. The scattering of light and the radial distribution function of high polymer solutions. Journal of Chemical Physics 16, 1093-1099 Ibid. Apparatus and methods for measurement and interpretation of the angular variation of light scattering; Preliminary results on polystyrene solutions. Journal of Chemical Physics 1948, 16, 1099-1116.
2 Wyatt, P. J. Light scattering and the absolute characterization of macromolecules. Analytica Chimica Acta 1993, 272, 1–40.
