Grundlagen CG-MALS
Lichtstreuung kann mehr als nur molare Masse und Größe. Sie ist auch ein großartiges Werkzeug zur Untersuchung makromolekularer Wechselwirkungen in Lösung ohne Einsatz von Markern oder Immobilisierung. In der Kompositionsgradienten-Mehrwinkel-Lichtstreuung (Composition-Gradient Multi-Angle Static Light Scattering, CG-MALS oder CG-SLS), werden die gleichen Detektoren wie in der Chromatographie verwendet: ein statisches Mehrwinkel-Lichtstreudetektor, oft in Kombination mit einem Differentialrefraktometer oder UV/Vis-Absorptionsspektrophotometer.
Anstelle einer kontinuierlich fließenden Chromatographie, die größengetrennte Proben liefert, verwendet CG-MALS das Calypso™ ein Multi-Spritzen-Pumpensystem. Das Calypso ist so programmiert, dass es Stop-Flow-Injektionen einer Reihe von genau definierten Konzentrationen oder Zusammensetzungen liefert. Bei jedem Schritt werden die nach der Equilibrierung erfassten Daten analysiert, um dynamische Gleichgewichtseigenschaften der Proben zu bestimmen: die Stöchiometrie und die
Bindungsaffinität KA spezifischer Komplexe und/oder thermodynamische Parameter wie Virialkoeffizienten im Falle unspezifischer Wechselwirkungen. Auch die Reaktionsgeschwindigkeiten können bei jedem Schritt analysiert werden, um kinetische Parameter wie die Michaelis-Konstante kM oder Assoziations-/Dissoziationsgeschwindigkeitskonstanten kon, koff zu bestimmen.
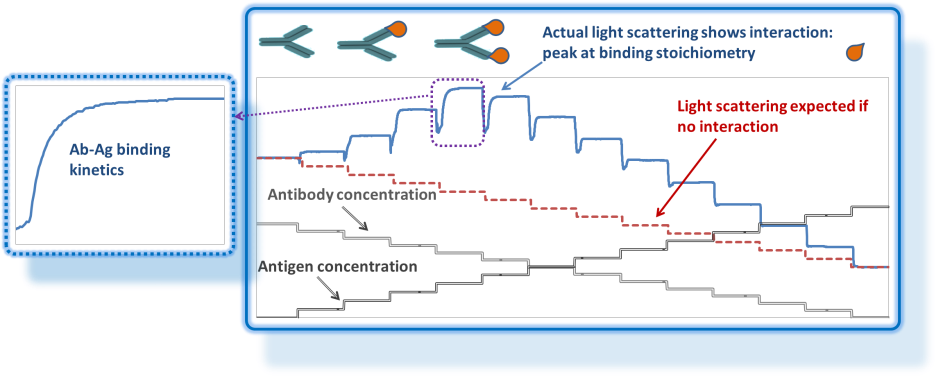
Konzeptionell ist CG-MALS eine absolute Technik, die vollständig auf ersten Prinzipien und thermodynamischen Grundlagen basiert. Da die statische Lichtstreuung die gewichtsmittlere molare Masse misst, liefert CG-MALS nicht nur das stöchiometrische Verhältnis, sondern die vollständige Stöchiometrie der Komplexe. Systeme, die Selbstwechselwirkungen, Hetero-Assoziationen oder sogar gleichzeitige reversible Selbst- und Hetero-Assoziationen eingehen, können quantifiziert werden. Eine besondere Stärke von CG-MALS ist die Analyse von Metakomplexen (z. B. die Selbstassoziation von einfachen Komplexen wie die Reaktion A+B+A+B↔AB+AB↔(AB)2). Die Analyse von Wechselwirkungen ist nicht auf Makromoleküle beschränkt, sondern kann auf das Verhalten größerer Objekte wie Liposomen oder Mikrogelpartikel einschließlich der an solchen Objekten haftenden Makromoleküle ausgedehnt werden. Dieselbe Instrumentierung kann dazu dienen, die Untersuchung zusätzlicher Phänomene wie die Abbaukinetik von Nanopartikeln zu automatisieren.
Weitere Details zu Theorie und Praxis von CG-MALS sowie eine Vielzahl von Beispielen finden Sie in "Characterization of Protein-Protein Interactions via Static and Dynamic Light Scattering", in Protein Interactions, ed. Jianfeng Cai und Rongsheng Wang, InTech, 2012. Die Publikation ist als Download hier frei verfügbar.
Eine weitere wertvolle Referenz zu Theorie und fortgeschrittenen Beispielen von CG-MALS ist "Light-scattering-based analysis of biomolecular interactions", als Open-Access-Download hier verfügbar.
Die folgenden Abschnitte enthalten einen Überblick über die Theorie hinter CG-MALS:
Spezifische Bindungen bei hoher Verdünnung
Im Idealfall der hohen Verdünnung kann die thermodynamische Nichtidealität, z. B. Virialkoeffiziententerme, ignoriert werden und die zeitlich gemittelte Lichtstreuintensität einer Lösung, die ein oder mehrere Makromoleküle enthält, wird durch diese Gleichung beschrieben:
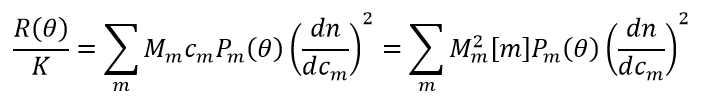
wobei:
- Mm, cm, Pm(θ) und dn/dcm sich auf die molare Masse, die Masse/Volumenkonzentration, die Winkelabhängigkeit aufgrund des endlichen Rg und den spezifischen Brechungsindex der molekularen Spezies m beziehen
- [m] ist die molare Konzentration der Spezies m
- R(θ) und K entsprechen den Definitionen in der klassischen Lichtstreuung, mit der Ausnahme, dass das dn/dc in K* enthalten ist, um einen probenunabhängigen Parameter K zu erhalten
Der Idealfall gilt typischerweise unterhalb von ~1 mg/mL Gesamtkonzentration für die meisten Proteine in einem Puffer mit angemessener Ionenstärke. Für andere Makromoleküle und Lösungsmittel kann der Gültigkeitsbereich variieren.
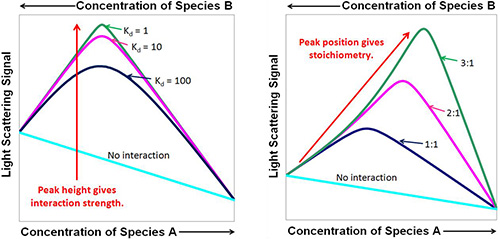
Innerhalb dieser Grenzen wird davon ausgegangen, dass ein reversibel assoziierendes System im dynamischen Gleichgewicht aus einem Gemisch aus 1) freien Monomeren A, B mit den Molmassen MA und MB bei den Konzentrationen [A] und [B]; and 2) gebundenen Komplexen Ai Bj mit der Molmasse Mij = iMA + jMB bei den Konzentrationen [Ai Bj] besteht. In Anlehnung an den Formalismus von Attri & Minton 20051, besteht die Datenanalyse aus der Kombination der idealen Lichtstreugleichung, die im Folgenden als (1) umgeschrieben wird, mit den Gleichungen für die Massenwirkung (2) und die Erhaltung der Masse (3):
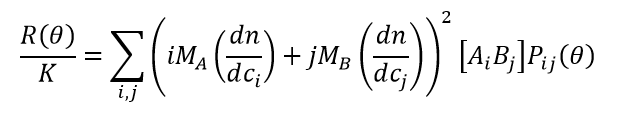 (1)
(1)
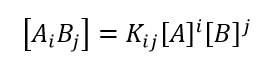 (2)
(2)
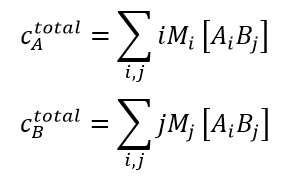 (3)
(3)
- Hier stehen A1 B0 und A0 B1 für die Monomere A und B; Ai B0 steht für das i-mere von A und A0Bj für j-mere von B.
- In Gl. (2) sind Kij die makroskopischen Gleichgewichtskonstanten für den Komplex ij
- In Gl. (3) sind cAtotal und cBtotal die gesamte Masse-/Volumenkonzentration von A und B, die gesamte Masse-/Volumenkonzentration von cAtotal und cBtotal werden direkt während eines CG-MALS-Experiments gemessen.
Literatur
1 Attri, A. K.; Minton, A. P. Composition gradient static light scattering: A new technique for rapid detection and quantitative characterization of reversible macromolecular hetero-associations in solution. Analytical Biochemistry 2005, 346, 132–138.
Unspezifische Wechselwirkungen, oder thermodynamische Nicht-Idealität
 Unspezifische Wechselwirkungen zwischen Makromolekülen entstehen aus einer Vielzahl von Quellen: Abstoßung im harten Kern, Abstoßung oder Anziehung aufgrund elektrostatischer Nettoladungen auf Moleküloberflächen, Anziehung aufgrund verschiedener Dipole und Terme höherer Ordnung (Monopol-Dipol, Dipol-Dipol, usw.), hydrophobe Bereiche bei Proteinen oder Peptiden, Hydratationskräfte, usw. Solche Wechselwirkungen werden durch das Lösungsmittel vermittelt und daher durch Ionenstärke und pH-Wert beeinflusst. Sie führen nicht zu einer spezifischen Schlüssel-Schloss-Bindung, um Komplexe mit wohldefinierter Stöchiometrie zu erzeugen, sondern erzeugen eine allgemeine Anziehung oder Abstoßung zwischen Makromolekülen. Unter relativ verdünnten Bedingungen, die sich dem Idealfall annähert aber diese nicht erreichen, werden unspezifische Selbstwechselwirkungen durch Virialkoeffizienten quantifiziert, insbesondere durch den zweiten Virialkoeffizienten A2 auch bekannt als B22 und den dritten Virialkoeffizienten A3 (B222). Die statische Lichtstreugleichung im verdünnten, nicht-idealen Bereich wird üblicherweise mit Gleichung 4 beschrieben:
Unspezifische Wechselwirkungen zwischen Makromolekülen entstehen aus einer Vielzahl von Quellen: Abstoßung im harten Kern, Abstoßung oder Anziehung aufgrund elektrostatischer Nettoladungen auf Moleküloberflächen, Anziehung aufgrund verschiedener Dipole und Terme höherer Ordnung (Monopol-Dipol, Dipol-Dipol, usw.), hydrophobe Bereiche bei Proteinen oder Peptiden, Hydratationskräfte, usw. Solche Wechselwirkungen werden durch das Lösungsmittel vermittelt und daher durch Ionenstärke und pH-Wert beeinflusst. Sie führen nicht zu einer spezifischen Schlüssel-Schloss-Bindung, um Komplexe mit wohldefinierter Stöchiometrie zu erzeugen, sondern erzeugen eine allgemeine Anziehung oder Abstoßung zwischen Makromolekülen. Unter relativ verdünnten Bedingungen, die sich dem Idealfall annähert aber diese nicht erreichen, werden unspezifische Selbstwechselwirkungen durch Virialkoeffizienten quantifiziert, insbesondere durch den zweiten Virialkoeffizienten A2 auch bekannt als B22 und den dritten Virialkoeffizienten A3 (B222). Die statische Lichtstreugleichung im verdünnten, nicht-idealen Bereich wird üblicherweise mit Gleichung 4 beschrieben:
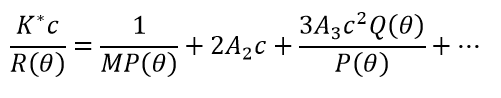 (4)
(4)
Oder
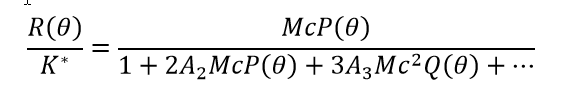 (5)
(5)
Sowohl P(θ) = 1 als auch Qθ = 1 gilt für Moleküle, die viel kleiner sind als die Wellenlänge des einfallenden Lichts, typischerweise mit Radien < 8 – 10 nm. Unspezifische Hetero-Wechselwirkungen werden zweckmäßigerweise durch Kreuzviralkoeffizienten, insbesondere A11 (B23), beschrieben. Es gibt verschiedene Formalismen zur Beschreibung der Lichtstreuung mit Eigen- und Kreuzviralkoeffizienten. Eine häufig verwendete Variante ist:
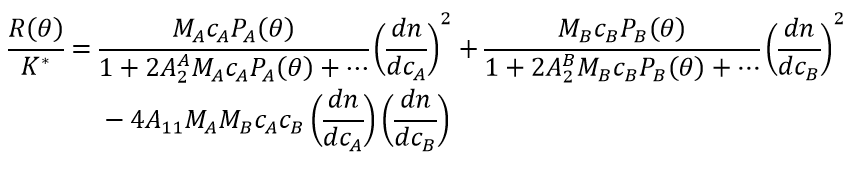 (6)
(6)
In diesen Gleichungen wird nicht nach stöchiometrischen Komplexen unterschieden; >c, cA und cB beziehen sich auf die Gesamtkonzentrationen der Probe.
Analysen bei hoher Konzentration, schwache oder quasi-spezifische Assoziation
Bei hohen Konzentrationen, typischerweise über 10 mg/mL und bis zu Hunderten von mg/mL für Proteine und ähnliche Makromoleküle, können schwache Wechselwirkungen, die verdünnte oder mäßig konzentrierte Lösungen nicht beeinflussen, wichtig werden. Die Analyse von CG-MALS-Daten, die bei solch hohen Konzentrationen erfasst wurden, wird durch das gleichzeitige Vorhandensein von abstoßenden Wechselwirkungen insbesondere die immer vorhandene Hard-Core-Abstoßung und einer Vielzahl von unspezifischen, anziehenden Wechselwirkungen erschwert. Glücklicherweise neigen abstoßende und anziehende Wechselwirkungen dazu, unterschiedliche Funktionsformen in ihrer Konzentrationsabhängigkeit zu erzeugen, wodurch sie gleichzeitig unterschieden und quantifiziert werden können.
Signale aus einer primär repulsiven Wechselwirkung werden oft gut durch das Effective Hard Sphere (EHS)-Modell1. EHS verwendet einen einzigen Parameter, das effektive spezifische Volumen veff, aus dem alle Virialkoeffizienten berechnet werden können, was das Anpassungsverfahren robust macht. Somit gilt für die Extrapolation auf den Winkel Null oder bei jedem Winkel für isotrope Streuer, also Moleküle mit einem Radius unter 8 - 10nm:
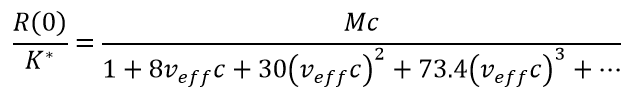 (7)
(7)
Minton beschriebt ein Modell für die Analyse hochkonzentrierter Selbstwechselwirkungen, indem er annimmt, dass die gesamte Anziehung als reversible Oligomerisierung beschrieben werden kann, während die gesamte Abstoßung in einem einzigen Parameter zusammengefasst werden kann: dem effektiven spezifischen Volumen veff das für Monomere und alle Oligomeren als gleich angenommen wird. Diese Oligomere sind möglicherweise keine echten spezifischen Komplexe mit robusten Stöchiometrien, sondern können als quasi-spezifische Oligomere mit ungefähren Stöchiometrien betrachtet werden, die sich bei veränderten Lösungsmittelbedingungen verschieben können. Der vollständige Algorithmus zur Anpassung von Hochkonzentrationsdaten an ein Selbstassoziationsmodell und zur Bestimmung der Stöchiometrie, der i-mer Gleichgewichtsassoziationskonstanten Ki und veff ist komplex. Einen vereinfachten Satz von Gleichungen, der das Wesentliche eines selbstassoziierenden Systems in Anwesenheit von (repulsiver) Nicht-Idealität angemessen wiedergibt, erhält man durch Kombination von Gleichung (7) mit den Gleichungen (1) - (3):
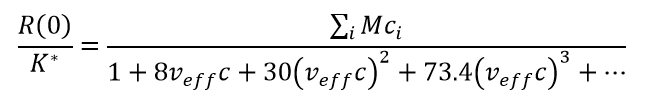 (8)
(8)
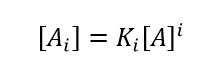 (9)
(9)
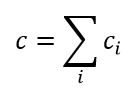 (10)
(10)
Literatur:
1 Minton, A. P. Light Scattering from Concentrated Protein Solutions, I: General Theory for Protein Mixtures and Application to Self-Associating Proteins. Biophysical Journal 2007, 93, 1321-1328.
Reaktions-Kinetik
Für die Lichtstreuung gilt die Standard-Reaktionskinetik der Lösung. Das Streusignal ist proportional zu dem Produkt aus Konzentration und molarer Masse, so dass die Daten durch einen entsprechenden Gleichungssatz beschrieben werden. Für den einfachen Fall von A+B↔AB, ergibt sich eine Kinetik 2ter Ordnung:
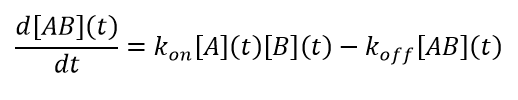 (11)
(11)
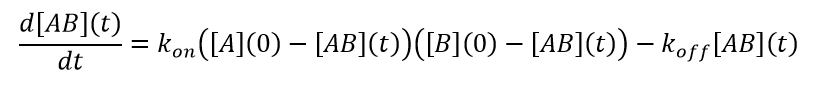 (12)
(12)
Die Zeitabhängigkeit der Streulichtintensität, extrapoliert auf den Winkel Null oder bei jedem Winkel für isotrope Streuer, also Teilchen mit Radius < 8 – 10 nm, ist:
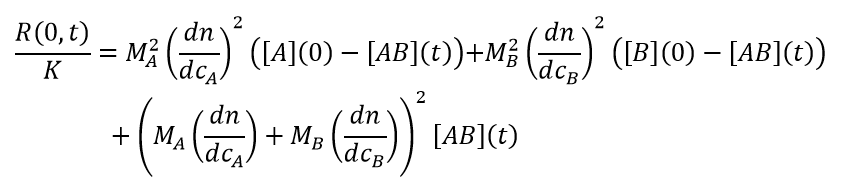 (13)
(13)


