Understanding Electrophoretic Light Scattering
Electrophoretic light scattering (ELS) is an optical technique for measuring electrophoretic mobility of particles in solution or suspension. In combination with knowledge of the particle’s hydrodynamic radius and other parameters, ELS enables determination of zeta potential and the effective charge.
Theory
ELS: electrophoretic mobility
Electrophoresis is the migration of macromolecules and dispersed particles under the influence of an electric field. The electrophoretic mobility µE is defined as:
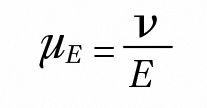 (1)
(1)
where v is the particle electrophoretic velocity, and E is the applied electric field.
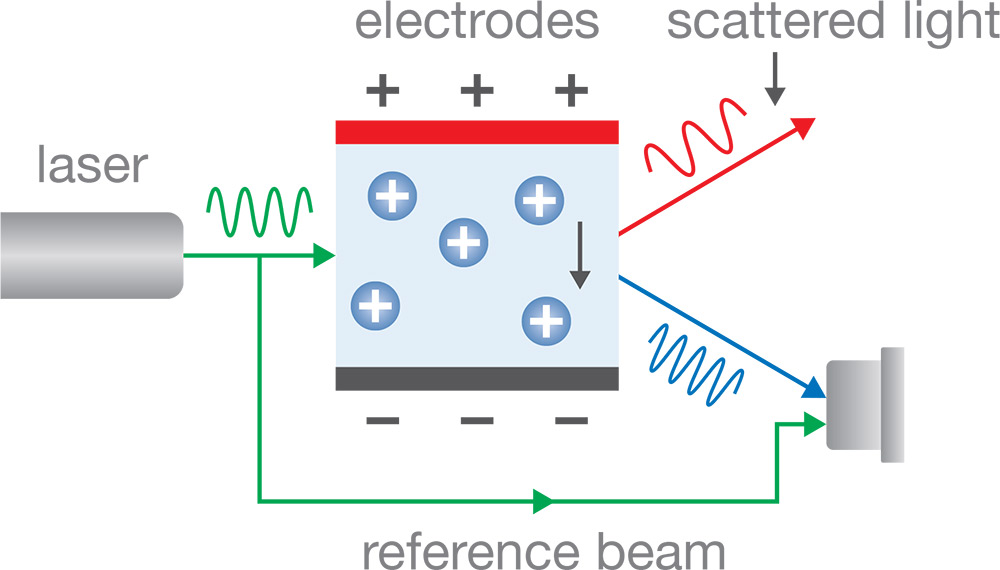
In ELS, a sample cell containing optical windows and electrodes is illuminated by a highly coherent laser beam. Upon applying voltage to the electrodes, particles migrate and attain a certain velocity, the magnitude and direction of which depend on the particle’s size and surface charge as well as solution viscosity and conductivity. This velocity causes the light scattered by the particles to be Doppler shifted, as illustrated to the right. The scattered light will be red- or blue-shifted (i.e., the optical frequency decreases or increases, respectively) depending on the direction of the particle migration relative to the scattering angle.
The Doppler frequency shift Δf of the scattered light which is related to v by:
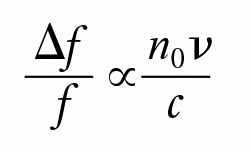 (2)
(2)
where:
c is the speed of light in vacuum.
n0 is the solvent refractive index.
f is the frequency of the incident light.
Even though the Doppler shift Δf of particles that can be measured by ELS is tiny compared with the light frequency (Δf/f < 0.000000000001!), it can be determined by means of interferometry. A split-off portion of the incident beam, known as the reference beam, is routed around the sample cell and combined with the incident light that has been scattered towards the detector. Interference between the two beams produces periodic intensity fluctuations on the detector at a frequency of Δf/f.
ELS + DLS: zeta potential and effective charge
Thanks to the independent dynamic light scattering module in the ZetaStar, the particle’s hydrodynamic radius Rhcan be measured simultaneously with mobility in order to compute the zeta potential, ζ and molecular charge. Zeta potential represents the electric potential around the particle at the slipping plane, i.e. the radius within which counterions attracted to the particle move with the particle, whereas outside that radius ions move independently of the particle.
In the limiting case where the hydrodynamic radius is much larger than the thickness of the ionic double layer, Smoluchowski's equation is used, per Equation 3:
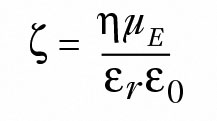 (3)
(3)
where η is the solution viscosity, εr is the solvent dielectric constant and ε0 the vacuum permittivity.
Alternately, when Rh is much smaller than the double layer thickness, Hückel's equation is used instead per Equation 4:
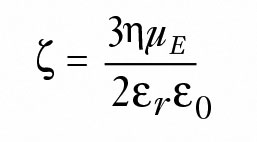 (4)
(4)
ZetaStar can also determine the molecular Debye-Hückel-Henry charge ZDHHe of the particle through the relationship in Equation 5:
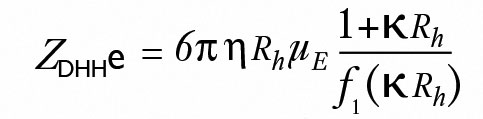 (5)
(5)
where κ is the inverse Debye length (calculated from the conductivity, σ, which is measured by the ZetaStar) and f1(κ Rh) is Henry's function*.
References
* Tanford, C. Physical Chemistry of Macromolecules; Wiley: New York, 1961.
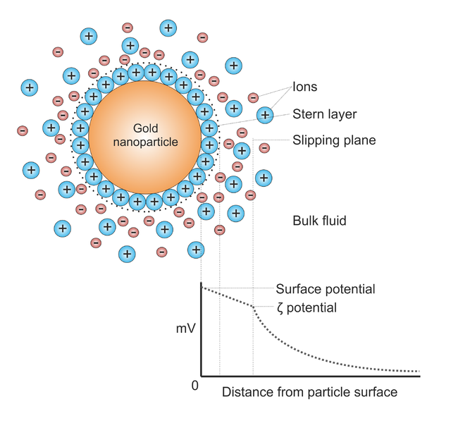
Diagram showing the ionic concentration and potential difference as a function of distance from the charged surface of a particle suspended in a dispersion medium. Larryisgood, CC BY-SA 3.0 https://creativecommons.org/licenses/by-sa/3.0, via Wikimedia Commons.
Technology
Conventional PALS
Intensity oscillations at the detector produced by Interference between the reference beam and scattered light is sufficient to determine the magnitude of Δf but not its sign, which conveys the sign of the zeta potential or charge. In order to ascertain the sign of Δf, conventional ELS utilizes a technique called phase-analysis light scattering (PALS) wherein a pair of oscillating mirrors impart an extra frequency shift to the reference beam. Tracking the relative phase between the mechanical motion of the mirrors and that of the detector signal provides the additional information required to determine the sign of Δf. However, the extra frequency is in the range of typical mechanical noise and the optical system itself requires exquisite adjustments in order to maintain alignment of the beams. These two concerns make conventional PALS relatively unreliable and possibly subject to the requirement of periodic maintenance.
FIDELIS
In order to overcome the deficiencies of conventional PALS, Wyatt developed a new technology, fiber interferometric Doppler electrophoretic light scattering (FIDELIS), implemented in the DynaPro™ ZetaStar™. In FIDELIS, the pair of moving mirrors are replaced by a coupled pair of acousto-optic modulators, which are devices that modulate the path length at much higher frequencies than is possible with the mechanical motion of mirrors. In fact, this system provides kHz-frequency modulation so the beat frequency at the detector is now fAOM+ Δf, where fAOM is the modulation frequency imparted by the acousto-optic modulators. The sign of Δf is inherently detected as the difference of the beat frequency relative to fAOM.
Furthermore, the entire FIDELIS optical system is fiber coupled such that the entire reference optical path is monolithic, with no free-space optics, as is coupling of the incident and scattered beams to and from the sample cell.
FIDELIS and the ZetaStar meet the needs of modern ELS instrumentation in two ways:
- High-frequency phase modulation moves the interferometric beats from ~ 100 Hz to ~ 10000 Hz, a range well outside that of mechanical noise, for high signal-to-noise ratio and sensitivity as well as inherent detection of the sign of Δf.
- Fiber-coupled optics effortlessly maintain most of the optical alignment and optical surface cleanliness. FIDELIS technology constitutes a set of field-replaceable modules for maximum instrument uptime and user productivity.
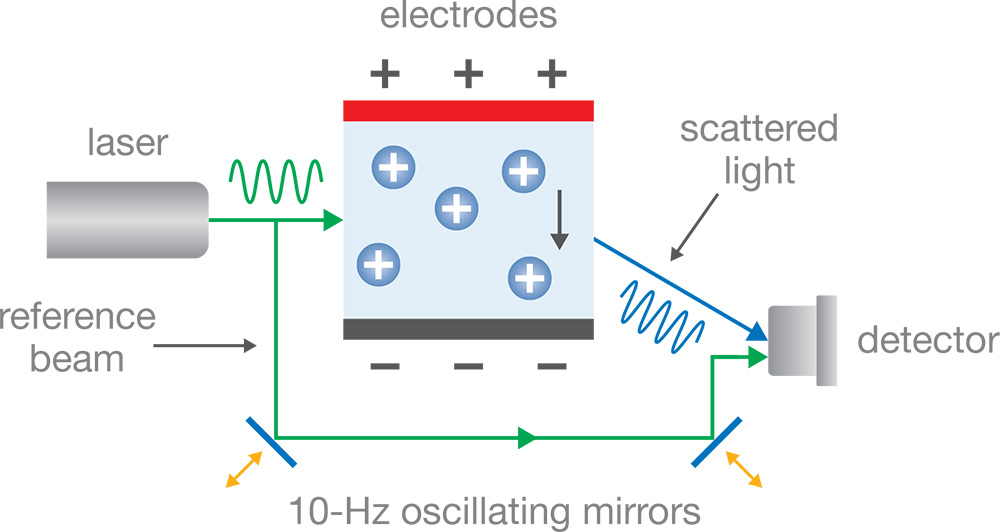
Figure 1: Conventional phase-analysis electrophoretic light scattering utilizes mechanically moving the mirrors to modulate the optical path length. Slight misalignments of the laser, mirrors and detector may impact the reliability of data.
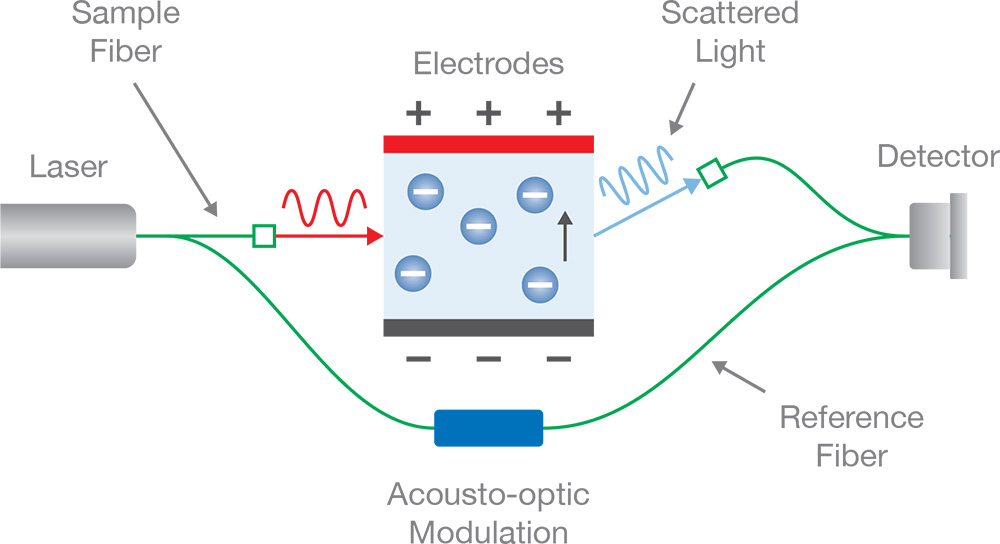
Figure 2: FIDELIS technology, utilized in the DynaPro ZetaStar, employs fiber-coupled elements: laser, splitter, acousto-optic modulator and beam combiner, for a robust and monolithic ELS optical system providing excellent sensitivity and speed.
